题目内容
5. 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 结合中位线的定义以及性质可得出“DF=BE,∠EDF=∠DEB”,再由△EDF和△DEB有条公共边利用SAS即可证得△DEF≌△EDB;同理即可证出:△DEF≌△CFE,△DEF≌△FAD.由此即可得出结论.
解答 解:∵D、E、F分别是AB、BC、CA的中点,
∴DF为△ABC的中位线,
∴DF∥BC,DF=BE=EC=$\frac{1}{2}$AB,
∴∠EDF=∠DEB.
在△EDF和△DEB中,
$\left\{\begin{array}{l}{DF=EB}\\{∠EDF=∠DEB}\\{DE=DE}\end{array}\right.$,
∴△DEF≌△EDB(SAS).
同理可证得:△DEF≌△CFE,△DEF≌△FAD.
故选D.
点评 本题考查了中位线的性质以及全等三角形的判定,解题的关键是根据中位线的性质找出相等的边及角.本题属于基础题,难度不大,解决该题型题目时,结合已知寻找相等的边和角是关键.

练习册系列答案
相关题目
12.若方程组$\left\{\begin{array}{l}{2a-3b=13}\\{3a+5b=30}\end{array}\right.$的解是$\left\{\begin{array}{l}{a=8.3}\\{b=1.2}\end{array}\right.$,则方程组$\left\{\begin{array}{l}{2(x+2)-3(y-1)=13}\\{3(x+2)+5(y-1)=30}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=8.3}\\{y=1.2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=10.3}\\{y=1.2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6.3}\\{y=2.2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=10.3}\\{y=0.2}\end{array}\right.$ |
 如图,在?ABCD中,AC与BD相交于点O,AE⊥BD于E,AF⊥BD于F,则图中的全等三角形共有6对.
如图,在?ABCD中,AC与BD相交于点O,AE⊥BD于E,AF⊥BD于F,则图中的全等三角形共有6对.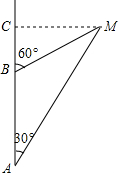 钓鱼岛自古就是中国的领土,中国有关部门己钓鱼岛及其附属岛屿开展常态化监视监测,一日,中国一艘海监船从A点沿正北方向以每小时24海里的速度巡航,在A点测得钓鱼岛中心M在点A的北偏东30°方向,问航行半小时后到达B点,测得钓鱼岛中心M在点B的北偏东60°方向,问再航行多少小时距离钓鱼岛中心最近?
钓鱼岛自古就是中国的领土,中国有关部门己钓鱼岛及其附属岛屿开展常态化监视监测,一日,中国一艘海监船从A点沿正北方向以每小时24海里的速度巡航,在A点测得钓鱼岛中心M在点A的北偏东30°方向,问航行半小时后到达B点,测得钓鱼岛中心M在点B的北偏东60°方向,问再航行多少小时距离钓鱼岛中心最近?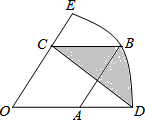 如图,在扇形EOD中,OD=3,菱形OABC的顶点A、B、C分别在OD、$\widehat{DE}$和OE上,OA=$\sqrt{3}$,连接CD,则阴影部分的面积为$\frac{3π-9+3\sqrt{3}}{4}$.
如图,在扇形EOD中,OD=3,菱形OABC的顶点A、B、C分别在OD、$\widehat{DE}$和OE上,OA=$\sqrt{3}$,连接CD,则阴影部分的面积为$\frac{3π-9+3\sqrt{3}}{4}$.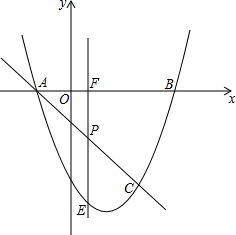 如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.
如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标. 由一些大小相同、边长为1cm的小正方形组成的几何体的三视图如图所示,那么这个几何体表面积是22cm2,体积是5cm3.
由一些大小相同、边长为1cm的小正方形组成的几何体的三视图如图所示,那么这个几何体表面积是22cm2,体积是5cm3.