题目内容
17.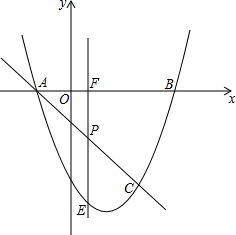 如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.
如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.
分析 令抛物线的y=0,求得x的值,较小的x值即为点A的横坐标,把点A坐标代入直线y=kx-1求得k的值,再把直线y=kx-1与抛物线y=x2-3x-4联立列出方程组即可得出答案.
解答 解:∵抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),
∴y=0,
∴x2-3x-4=0,
∴x1=4,x2=-1,
∴A(-1,0),B(4,0),
把x=-1代入y=kx-1得k=-1,
∴直线的解析式为y=-x-1,
∴$\left\{\begin{array}{l}{y=-x-1}\\{y={x}^{2}-3x-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=-4}\end{array}\right.$,
∴A(-1,0),C(3,-4),
∴A,B,C三点的坐标分别为A(-1,0),B(4,0),C(3,-4).
点评 本题考查了抛物线与x轴的交点坐标,主要利用了联立两函数解析式求交点问题,求出直线解析式是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
5. 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
4.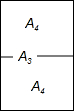 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
 复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号有A0、A1、A2、A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )| A. | 2:1 | B. | $\sqrt{2}$:1 | C. | $\sqrt{3}$:1 | D. | 3:1 |
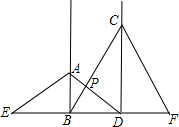 如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?
如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?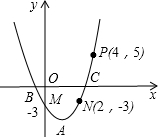 如图抛物线y=ax2+bx+c(a≠0)过M,N,P三点.
如图抛物线y=ax2+bx+c(a≠0)过M,N,P三点.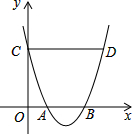 如图,对称轴平行于y轴的抛物线与x轴交于点A、B,与y轴交于点C,过C作CD∥x轴,与抛物线交于点D.若OA=1,CD=4,则线段AB的长为2.
如图,对称轴平行于y轴的抛物线与x轴交于点A、B,与y轴交于点C,过C作CD∥x轴,与抛物线交于点D.若OA=1,CD=4,则线段AB的长为2.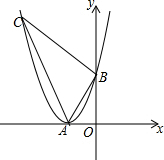 如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.
如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.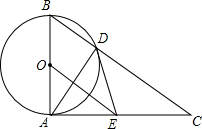 如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.