题目内容
20.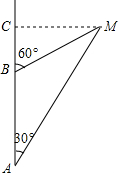 钓鱼岛自古就是中国的领土,中国有关部门己钓鱼岛及其附属岛屿开展常态化监视监测,一日,中国一艘海监船从A点沿正北方向以每小时24海里的速度巡航,在A点测得钓鱼岛中心M在点A的北偏东30°方向,问航行半小时后到达B点,测得钓鱼岛中心M在点B的北偏东60°方向,问再航行多少小时距离钓鱼岛中心最近?
钓鱼岛自古就是中国的领土,中国有关部门己钓鱼岛及其附属岛屿开展常态化监视监测,一日,中国一艘海监船从A点沿正北方向以每小时24海里的速度巡航,在A点测得钓鱼岛中心M在点A的北偏东30°方向,问航行半小时后到达B点,测得钓鱼岛中心M在点B的北偏东60°方向,问再航行多少小时距离钓鱼岛中心最近?
分析 先求出AB的长,设BC=x海里,用x表示出CM的长,在Rt△ACM中根据锐角三角函数的定义即可得出结论.
解答 解:∵海监船从A点沿正北方向以每小时24海里的速度巡航,航行半小时后到达B点,
∴AB=12海里.
设BC=x海里,
∵∠MBC=60°,MC⊥AC,
∴CM=BC•tan60°=$\sqrt{3}$x.
在Rt△ACM中,
∵∠A=30°,
∴$\frac{CM}{AC}$=tan30°,即$\frac{\sqrt{3}x}{12+x}$=$\frac{\sqrt{3}}{3}$,解得x=6(海里),
∴t=$\frac{6}{24}$=0.25(小时).
答:再航行0.25小时距离钓鱼岛中心最近.
点评 本题考查的是解直角三角形的应用,根据题意利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
5. 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,图中与△DEF全等的三角形有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |

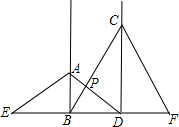 如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?
如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?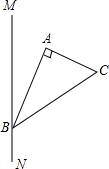 如图所示,一条南北方向的小路MN,A、B、C处各有一颗小树,且B在MN上,∠A=90°,A、C之间的距离为200米,在B处测得C在小路的北偏东55°方向上,A在小路的北偏东25°方向上,求点A到小路MN的距离.(结果精确到0.1米)
如图所示,一条南北方向的小路MN,A、B、C处各有一颗小树,且B在MN上,∠A=90°,A、C之间的距离为200米,在B处测得C在小路的北偏东55°方向上,A在小路的北偏东25°方向上,求点A到小路MN的距离.(结果精确到0.1米)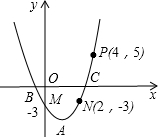 如图抛物线y=ax2+bx+c(a≠0)过M,N,P三点.
如图抛物线y=ax2+bx+c(a≠0)过M,N,P三点.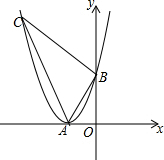 如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.
如图,抛物线y=ax2+bx+c的顶点A在轴上,与y轴的交点为B(0,4),且ac=b.平移直线y=-3x,使它经过点A,与抛物线的另一个交点为C.