题目内容
7.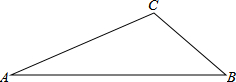 如图,已知△ABC
如图,已知△ABC(1)用直尺和圆规作出⊙O,使⊙O经过A,C两点,且圆心O在AB上(不写作法,保留作图痕迹)
(2)若AB=$\sqrt{2}$,BC=2-$\sqrt{2}$,∠B=45°,求出(1)中⊙O的半径R的值.
分析 (1)作AC的垂直平分线,则此垂直平分线与AB的交点为O,然后以O点为圆心,OA为半径作⊙O即可;
(2)作CH⊥AB于H,连结OC,先判断△BCH为等腰直角三角形,则BH=CH=$\frac{\sqrt{2}}{2}$BC=$\sqrt{2}$-1,所以AH=AB-BH=1,OH=AH-OA=1-R,然后在Rt△OCH中根据勾股定理得到(1-R)2+($\sqrt{2}$-1)2=R2,再解方程即可.
解答 解:(1)如图,⊙为所求;
(2)作CH⊥AB于H,连结OC,如图,
在Rt△BCH中,∵∠B=45°,
∴△BCH为等腰直角三角形,
∴BH=CH=$\frac{\sqrt{2}}{2}$BC=$\frac{\sqrt{2}}{2}$×(2-$\sqrt{2}$)=$\sqrt{2}$-1,
∴AH=AB-BH=$\sqrt{2}$-($\sqrt{2}$-1)=1,
∴OH=AH-OA=1-R,
在Rt△OCH中,∵OH2+CH2=OC2,
∴(1-R)2+($\sqrt{2}$-1)2=R2,
∴R=2-$\sqrt{2}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
13.电流通过导线时会产生热量,电流,(单位:A)、导线电阻R(单位:Q)、通电时间t(单位:s)与产生的热量Q(单位:J)满足Q=I2Rt.已知导线的电阻为5Ω,1s时间导线产生30J的热量,则I的值为( )
| A. | 2.4A | B. | $\sqrt{6}$A | C. | 4.8A | D. | 5$\sqrt{6}$A |
2.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表所示.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表
从上表可知,下列说法正确的个数为( )
①抛物线与x轴的一个交点为(-2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=$\frac{1}{2}$;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减小.
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -6 | 0 | 4 | 6 | 6 | … |
①抛物线与x轴的一个交点为(-2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=$\frac{1}{2}$;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减小.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.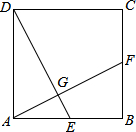 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
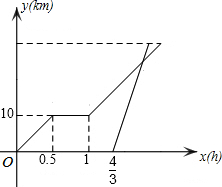 周末,小明和同学一起骑自行车从家里出发到巢湖湿地公园郊游,从家出发0.5小时后到达天鹅湖,游玩一段时间后按原速前往巢湖湿地公园.小明离家80分钟后,妈妈驾车沿相同路线前往巢湖湿地公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
周末,小明和同学一起骑自行车从家里出发到巢湖湿地公园郊游,从家出发0.5小时后到达天鹅湖,游玩一段时间后按原速前往巢湖湿地公园.小明离家80分钟后,妈妈驾车沿相同路线前往巢湖湿地公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.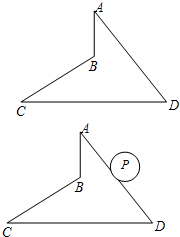 如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.
如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10. 在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1.
在RtABC中,∠C=90°,AC=BC=$\sqrt{2}$(如图),若将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,联结C′B,则C′B的长为$\sqrt{3}$-1. 如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.
如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.