题目内容
5.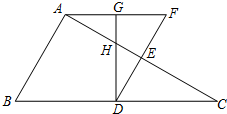 如图,△ABC中,BC=2AB,点D、E分别是BC、AC的中点,过点A作AF∥BC交线段DE的延长线于点F,取AF的中点G,联结DG,GD与AE交于点H.
如图,△ABC中,BC=2AB,点D、E分别是BC、AC的中点,过点A作AF∥BC交线段DE的延长线于点F,取AF的中点G,联结DG,GD与AE交于点H.(1)求证:四边形ABDF是菱形;
(2)求证:DH2=HE•HC.
分析 (1)首先根据三角形的中位线定理,得DE∥AB,结合AF∥BC,根据两组对边分别平行的四边形是平行四边形,可以判断该四边形是平行四边形,再根据一组邻边相等的平行四边形是菱形即可证明;
(2)根据菱形的性质可以进一步得到△FGD≌△FEA,则GD=AE,然后通过证明三角形相似,即可得到结论.
解答 (1)证明:∵点D、E分别是BC、AC的中点
∴DE∥AB,BC=2BD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∵BC=2AB,
∴AB=BD,
∴四边形ABDF是菱形;
(2)证明:∵四边形ABDF是菱形,
∴AF=DF,
∵点G是AF的中点,
∴FG=$\frac{1}{2}$AF,
∵点E是AC的中点,
∴AE=CE,
∵AF∥BC,
∴$\frac{EF}{DE}$=$\frac{AE}{CE}$=1,
∴EF=$\frac{1}{2}$DF,
∴FG=EF,
在△AFE和△DFG中
$\left\{\begin{array}{l}{AF=DF}\\{∠F=∠F}\\{EF=GF}\end{array}\right.$,
∴△AFE≌△DFG,
∴∠FAE=∠FDG,
∵AF∥BC,
∴∠FAE=∠C,
∴∠FDG=∠C,
又∵∠EHD=∠DHC,
∴△HED∽△HDC,
∴$\frac{HE}{HD}$=$\frac{HD}{HC}$,
∴DH2=HE•HC.
点评 本题考查了三角形的中位线定理、菱形的判定和性质、全等三角形的判定和性质,相似三角形的判定和性质,熟记定理是解题的关键.

练习册系列答案
相关题目
20.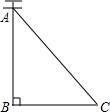 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
 如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )
如图,AC是电线杆AB的一根拉线,测得BC的长为6米,∠ACB=50°,则拉线AC的长为( )| A. | $\frac{6}{sin50°}$米 | B. | $\frac{6}{tan50°}$米 | C. | 6cos50°米 | D. | $\frac{6}{cos50°}$米 |
17.下面几组数:①7,8,9;②12,9,15;③a2,a2+1,a2+2;④m2+n2,m2-n2,2mn(m、n均为正整数,m>n),其中能组成直角三角形的三边长的是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
15.如果分式$\frac{2x}{x-y}$中的x、y都缩小到原来的$\frac{1}{3}$倍,那么分式的值( )
| A. | 扩大到原来的3倍 | B. | 扩大到原来的6倍 | ||
| C. | 不变 | D. | 缩小到原来的$\frac{1}{3}$倍 |
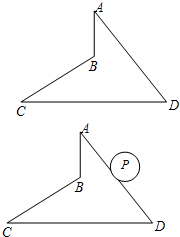 如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.
如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10. 如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.
如图所示,三角形OAB的顶点B的坐标为(4,0),把三角形OAB沿x轴向右平移得到三角形CDE,如果CB=1,那么OE的长为7.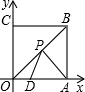 如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为2$\sqrt{10}$.
如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为2$\sqrt{10}$. 将一个含30°的角的直角三角尺,∠AMF=90°,如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为15°.
将一个含30°的角的直角三角尺,∠AMF=90°,如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为15°.