题目内容
3. 甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )
甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )| A. | 甲的速度为60千米/小时 | B. | 乙从A地到B地用了3小时 | ||
| C. | 甲比乙晚出发0.5小时 | D. | 甲到达B地时,乙离A地80千米 |
分析 根据图象得出信息,然后利用待定系数法求出CD、OE的解析式进行解答判断即可.
解答 解:设甲的解析式为y=kx+b,可得:
$\left\{\begin{array}{l}{120=2k+b}\\{40=k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=80}\\{b=-40}\end{array}\right.$,
所以解析式为:y=80x-40,
把y=0代入解析式中,可得:0=80x-40,
解得:x=0.5,
所以甲的速度为:120÷(2-0.5)=80,故A错误;
由图象可得乙的速度为:40÷1=40,所以乙的时间为:120÷40=3小时,故B正确;
甲比乙晚0.5小时,故C正确;
甲到达B地时,乙离A地2×40=80千米,故D正确;
故选A.
点评 本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,准确识图并获取信息是解题的关键.

练习册系列答案
相关题目
9.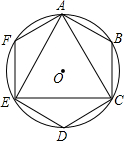 在等边△ACE内接于⊙O,连接B,D,F分别是$\widehat{AB}$,$\widehat{CE}$,$\widehat{AE}$的中点,连接AB,BC,CD,DE,EF,FA.将该图形绕点O旋转一个合适的角度后会与原图形重合,则这个旋转角的度数可能是( )
在等边△ACE内接于⊙O,连接B,D,F分别是$\widehat{AB}$,$\widehat{CE}$,$\widehat{AE}$的中点,连接AB,BC,CD,DE,EF,FA.将该图形绕点O旋转一个合适的角度后会与原图形重合,则这个旋转角的度数可能是( )
 在等边△ACE内接于⊙O,连接B,D,F分别是$\widehat{AB}$,$\widehat{CE}$,$\widehat{AE}$的中点,连接AB,BC,CD,DE,EF,FA.将该图形绕点O旋转一个合适的角度后会与原图形重合,则这个旋转角的度数可能是( )
在等边△ACE内接于⊙O,连接B,D,F分别是$\widehat{AB}$,$\widehat{CE}$,$\widehat{AE}$的中点,连接AB,BC,CD,DE,EF,FA.将该图形绕点O旋转一个合适的角度后会与原图形重合,则这个旋转角的度数可能是( )| A. | 60° | B. | 90° | C. | 120° | D. | 180° |
11.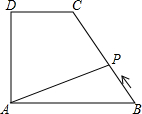 如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
 如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )| A. | 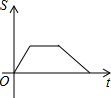 | B. | 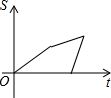 | C. | 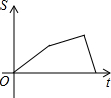 | D. | 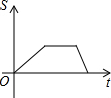 |
8.台湾是我国最大的岛屿,总面积为35989.76平方千米.用科学记数法应表示为(保留三个有效数字)( )平方千米.
| A. | 3.59×106 | B. | 3.60×106 | C. | 3.59×104 | D. | 3.60×104 |
12.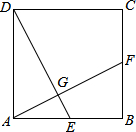 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
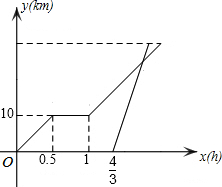 周末,小明和同学一起骑自行车从家里出发到巢湖湿地公园郊游,从家出发0.5小时后到达天鹅湖,游玩一段时间后按原速前往巢湖湿地公园.小明离家80分钟后,妈妈驾车沿相同路线前往巢湖湿地公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
周末,小明和同学一起骑自行车从家里出发到巢湖湿地公园郊游,从家出发0.5小时后到达天鹅湖,游玩一段时间后按原速前往巢湖湿地公园.小明离家80分钟后,妈妈驾车沿相同路线前往巢湖湿地公园,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.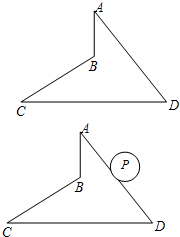 如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.
如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.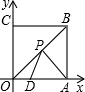 如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为2$\sqrt{10}$.
如图,正方形OABC的边长为6,点A、C分别在x轴,y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为2$\sqrt{10}$.