题目内容
20.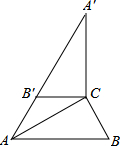 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )| A. | 6 | B. | $4\sqrt{3}$ | C. | $3\sqrt{3}$ | D. | 3 |
分析 根据直角三角形的性质,可得AB的长,根据旋转的性质,可得A′B′的长,B′C的长,∠A′、∠A′B′C′,根据邻补角的定义,可得∠AB′C的度数,根据等腰三角形的判定,可得AB′,根据线段的和差,可得答案.
解答 解:由在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,得
AB=4,∠BAC=30°.
由旋转的性质,得
A′B′=AB=4,∠A′=∠BAC=30°,∠A′B′C=∠B=60°,AC=A′C.
由等腰三角形的性质,得
∠CAB′=∠A′=30°.
由邻补角的定义,得
∠AB′C=180°-∠A′B′C=120°.
由三角形的内角和定理,得
∠ACB′=180°-∠AB′C-∠B′AC=30°.
∴∠B′AC=∠B′CA=30°,
AB′=B′C=BC=2.
A′A=A′B′+AB′=4+2=6,
故选:A.
点评 本题考查了旋转的性质,利用了旋转的性质,直角三角形的性质,等腰三角形的性质,利用等腰三角形的判定得出AB′=B′′C是解题关键.

练习册系列答案
相关题目
11.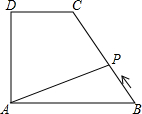 如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
 如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )| A. | 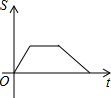 | B. | 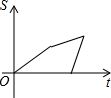 | C. | 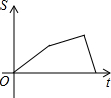 | D. | 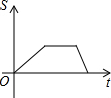 |
8.台湾是我国最大的岛屿,总面积为35989.76平方千米.用科学记数法应表示为(保留三个有效数字)( )平方千米.
| A. | 3.59×106 | B. | 3.60×106 | C. | 3.59×104 | D. | 3.60×104 |
5.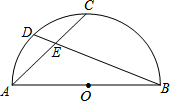 如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,点D是$\widehat{AC}$的中点,连接AC、BD交于点E,则$\frac{DE}{BE}$=( )
如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,点D是$\widehat{AC}$的中点,连接AC、BD交于点E,则$\frac{DE}{BE}$=( )
 如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,点D是$\widehat{AC}$的中点,连接AC、BD交于点E,则$\frac{DE}{BE}$=( )
如图,AB是半圆O的直径,点C是$\widehat{AB}$的中点,点D是$\widehat{AC}$的中点,连接AC、BD交于点E,则$\frac{DE}{BE}$=( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{16}$ | C. | 1-$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}-1}{2}$ |
12.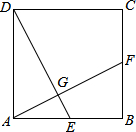 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
 如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )
如图,在正方形ABCD中,点E为AB的中点,AF⊥DE于点G,则$\frac{GA}{GD}$等于( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
9. 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
 如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )
如图,在平行四边形ABCD中,E为CD上一点,连AE、BD,且AE、BD交于点F,若DE:EC=2:3,则S△DEF:S△ABF等于( )| A. | $\frac{4}{25}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
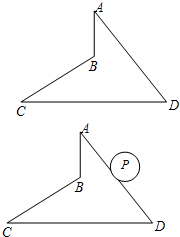 如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10.
如图,四边形ABCD中,已知∠A=∠C=30°,∠D=60°,AD=8,CD=10. 将一个含30°的角的直角三角尺,∠AMF=90°,如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为15°.
将一个含30°的角的直角三角尺,∠AMF=90°,如图所示放置在矩形纸板上,已知矩形纸板的长是宽的2倍,点M是BC边的中点,则∠AFE的度数为15°.