题目内容
11.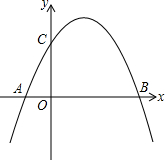 如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.
如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.(1)求抛物线的解析式;
(2)若过点P(0,4)的直线(不与x轴,y轴平行)与抛物线只有一个交点,求该直线的解析式.
分析 (1)设A(t,0),则B(t+4,0),则得到交点式y=-(x-t)(x-t-4),然后把C点坐标代入求出t即可得到抛物线解析式;
(2)设过P点的直线解析式为y=kx+4,由直线y=kx+4与抛物线只有一个交点得到方程-x2+2x+3=kx+4有相等的实数解,然后利用判别式的意义求出k的值即可.
解答 解:(1)设A(t,0),则B(t+4,0),
设抛物线解析式为y=-(x-t)(x-t-4),
把C(0,3)代入得-(-t)•(-t-4)=3,
整理得t2+4t+3=0,解得t1=-1,t2=-3(舍去),
所以抛物线解析式为y=-(x+1)(x-3),即y=-x2+2x+3;
(2)设过P点的直线解析式为y=kx+4,
因为直线y=kx+4与抛物线只有一个交点,
所以方程-x2+2x+3=kx+4有相等的实数解,
方程整理为x2+(k-2)x+1=0,
则△=(k-2)2-4=0,解得k=0(舍去)或k=4,
所以该直线的解析式为y=4x+4.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决(2)小题的关键是利用判别式的意义判断直线与抛物线的交点个数.

练习册系列答案
相关题目
19. 由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
 由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.
由一些大小相同的小正方体组成的几何体主视图和俯视图如图所示,小正方体的块数可能有( )种.| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
16.一辆出租车从某地出发,在一条东西走向的接到上往返行驶,每次行驶的路程(记向东为正),记录如下(8<x<24,单位:km);
(1)说出这辆出租车每次行驶的方向;
(2)这辆出租车一共行驶了多少路程(用含x的式子表示)?
| 第一次 | 第二次 | 第三次 | 第四次 |
| x | 3(8-x) | x-6 | -$\frac{2}{3}$x |
(2)这辆出租车一共行驶了多少路程(用含x的式子表示)?
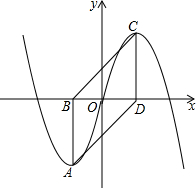 如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.
如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.
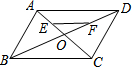 如图,在平行四边形ABCD中,AC与BD相交于点O,点E、F分别是OA、OD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BO}$=$\overrightarrow{b}$,那么$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.
如图,在平行四边形ABCD中,AC与BD相交于点O,点E、F分别是OA、OD的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BO}$=$\overrightarrow{b}$,那么$\overrightarrow{EF}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.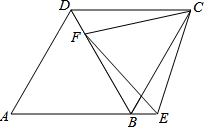 如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:
如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证: