题目内容
6.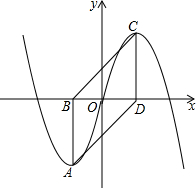 如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.
如图,在平面直角坐标系中,过抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点A作AB⊥x轴于点B,过抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点C作CD⊥x轴于点D,连结AD、BC.则四边形ABCD的面积为4.
分析 根据题意知道两个抛物线关于原点对称,从而判断四边形ABCD的形状为平行四边形,然后根据抛物线的顶点坐标确定CD和BD的长,利用平行四边形的面积计算方法确定面积即可.
解答 解:∵抛物线y=a(x+1)2-2(x≤0,a为常数)与抛物线y=-a(x-1)2+2(x≥0,a为常数)关于原点对称,
∴四边形ABCD为平行四边形,
∵抛物线y=a(x+1)2-2(x≤0,a为常数)的顶点坐标为(-1,-2),抛物线y=-a(x-1)2+2(x≥0,a为常数)的顶点坐标为(1,2),
∴BD=2,CD=2,
∴S四边形ABCD=BD×CD=2×2=4,
故答案为:4.
点评 本题考查了二次函数的性质,解题的关键是根据题意确定四边形ABCD的形状,难度不大.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
14.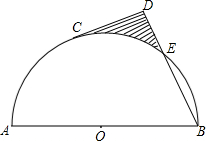 如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
 如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )
如图,点C在半圆0上,直径AB=8,$\widehat{BC}$=2$\widehat{AC}$,过点C作切线CD,BD⊥CD,则阴影部分的面积是( )| A. | 8$\sqrt{3}$-4π | B. | 8$\sqrt{3}$-$\frac{8}{3}$π | C. | 4π-6$\sqrt{3}$ | D. | 6$\sqrt{3}$-$\frac{8}{3}$π |
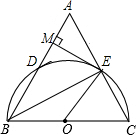 如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,过点E作半圆O的切线,交AB于M,连接BE.
如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,过点E作半圆O的切线,交AB于M,连接BE.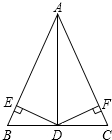 如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.
如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,垂足分别为E、F,且DE=DF.请选择一对你认为全等的三角形并加以证明.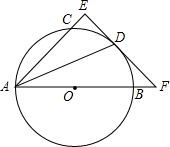 如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.
如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.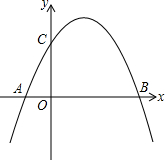 如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.
如图,抛物线y=-x2+bx+c与x轴交于AB两点(A在B的左侧),与y轴相交于点C(0,3),抛物线的顶点在第一象限,AB=4.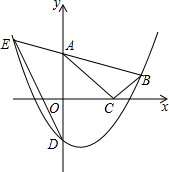 如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.
如图,在平面直角坐标系中,Rt△ABC的顶点A、C分别在y轴、x轴上,∠ACB=90°,OA=$\sqrt{3}$,抛物线y=ax2-ax-a经过点B(2,$\frac{\sqrt{3}}{3}$),与y轴交于点D.