题目内容
13.先化简,再求值:$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-xy}÷(\frac{x}{y}-\frac{y}{x})$,其中x,y满足$\left\{\begin{array}{l}{2x-y=5}\\{4x+y=1}\end{array}\right.$.分析 先根据分式混合运算的法则把原式进行化简,再求出x、y的值代入进行计算即可.
解答 解:原式=$\frac{(x-y)^{2}}{x(x-y)}$•$\frac{(x+y)(x-y)}{xy}$
=$\frac{x-y}{x}$•$\frac{xy}{(x+y)(x-y)}$
=$\frac{y}{x+y}$.
解方程组$\left\{\begin{array}{l}2x-y=5\\ 4x+y=1\end{array}\right.$得,$\left\{\begin{array}{l}x=1\\ y=-3\end{array}\right.$,
故原式=$\frac{-3}{1-3}$=$\frac{3}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
3.下列各式计算正确的是( )
| A. | a3+a4=a7 | B. | (3a+b)2=9a2+b2 | C. | (-ab3)2=a2b6 | D. | a6b÷a2=a3b |
8.函数y=$\frac{3}{\sqrt{x+2}}$中,自变量x的取值范围是( )
| A. | x≠-2 | B. | x≥-2 | C. | x>-2 | D. | x>2 |
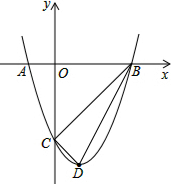 如图,抛物线y=x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3),点D为顶点,连接BC、BD、CD.
如图,抛物线y=x2+bx+c与x轴交于A、B(3,0)两点,与y轴交于点C(0,-3),点D为顶点,连接BC、BD、CD.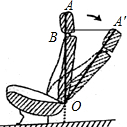 如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O顺时针旋转35°到OA′处,此时点A′到OA的距离为线段A′B的长,求调整后点A′比调整前点A降低的高度AB.(结果取整数)【参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70】
如图,这是一把可调节座椅的侧面示意图,已知头枕上的点A到调节器点O处的距离为80cm,AO与地面垂直,现调整靠背,把OA绕点O顺时针旋转35°到OA′处,此时点A′到OA的距离为线段A′B的长,求调整后点A′比调整前点A降低的高度AB.(结果取整数)【参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70】