题目内容
20.(sin45°)2+(-$\frac{1}{2}$)0-${12^{\frac{1}{2}}}$•${({\sqrt{3}-1})^{-1}}$+cot30°.分析 依据特殊角的三角函数值、零指数幂、分数值数幂、负整数指数幂化简各式,再根据分式的性质、分母有理化进一步化简可得.
解答 解:原式=$(\frac{\sqrt{2}}{2})^{2}$+1-$\sqrt{12}$×$\frac{1}{\sqrt{3}-1}$+$\sqrt{3}$
=$\frac{1}{2}$+1-2$\sqrt{3}$×$\frac{\sqrt{3}+1}{2}$+$\sqrt{3}$
=$\frac{3}{2}$-$\sqrt{3}(\sqrt{3}+1)$+$\sqrt{3}$
=$\frac{3}{2}$-3-$\sqrt{3}$+$\sqrt{3}$
=-$\frac{3}{2}$.
点评 本题主要考查分式的混合运算能力,掌握混合运算的运算顺序是根本、前提,准确计算特殊角的三角函数值、零指数幂、分数值数幂、负整数指数幂是解题的关键.

练习册系列答案
相关题目
8.函数y=$\frac{3}{\sqrt{x+2}}$中,自变量x的取值范围是( )
| A. | x≠-2 | B. | x≥-2 | C. | x>-2 | D. | x>2 |
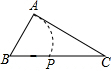
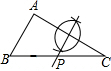
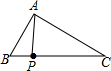
 如图,在钝角△ABC中,AC<BC,用尺规在BC上确定一点P,使PA+PC=BC,下面是四个同学的作法(只留下了作图痕迹,未连接PA),其中正确的是( )
如图,在钝角△ABC中,AC<BC,用尺规在BC上确定一点P,使PA+PC=BC,下面是四个同学的作法(只留下了作图痕迹,未连接PA),其中正确的是( )