题目内容
20．抛物线y=ax2+bx+c（a≠0），对称轴为直线x=2，且经过点P（3，0），则a+b+c的值为（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 3 |
分析 根据二次函数对称性可求出点（3，0）关于对称轴直线x=2的对称点为（1，0），然后把（1，0）代入y=ax2+bx+c即可求出答案．
解答 解：∵抛物线y=ax2+bx+c的对称轴为2，
∴根据二次函数的对称性得：点（3，0）的对称点为（1，0），
∵当x=1时，y=a+b+c=0，
∴a+b+c的值等于0．
故选B．
点评 本题主要考查了二次函数的性质，解答本题的关键是求出点P关于对称轴的对称点，此题难度不大．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
如图，在平面直角坐标系中，矩形OABC的顶点O为原点，E为AB上一点，把△CBE沿CE折叠，使点B恰好落在OA边上的点D处，A、D的坐标分别为（5，0）和（3，0）．
如图，在一块边长为a的正方形纸片的四角各剪去一个边长为b的正方形，若a=3.6，b=0.8，则剩余部分的面积为10.4．
5．
如图所示，一根树在离地面9米处断裂，树的顶部落在离底部12米处．树折断之前（ ）米．
如图所示，一根树在离地面9米处断裂，树的顶部落在离底部12米处．树折断之前（ ）米．| A． | 15 | B． | 20 | C． | 3$\sqrt{7}$ | D． | 24 |
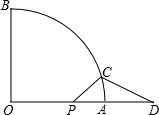如图，线段PA=1，点D是线段PA延长线上的点，AD=a（a＞1），点O是线段AP延长线上的点，OA2=OP•OD，以O为圆心，OA为半径作扇形OAB，∠BOA=90°．