题目内容
11. 如图,在平面直角坐标系中,矩形OABC的顶点O为原点,E为AB上一点,把△CBE沿CE折叠,使点B恰好落在OA边上的点D处,A、D的坐标分别为(5,0)和(3,0).
如图,在平面直角坐标系中,矩形OABC的顶点O为原点,E为AB上一点,把△CBE沿CE折叠,使点B恰好落在OA边上的点D处,A、D的坐标分别为(5,0)和(3,0).(1)已知抛物线y=2x2+bx+c经过B、D两点,求此抛物线的解析式;
(2)点P为线段CE上的动点,连接AP,当△PAE的面积为$\frac{27}{20}$时,求tan∠APE的值;
(3)将抛物线y=2x2+bx+c平移,使其经过点C,设抛物线与直线BC的另一个交点为M,问在该抛物线上是否存在点Q,使得△CMQ为等边三角形?若存在,求出点Q的坐标;若不存在,请说明理由;并直接写出满足(2)的P点是否在此时的抛物线上.
分析 (1)先在RT△CDO中求出CO,设BE=DE=x,在RT△ADE中利用勾股定理求出x,即可得到B、D两点坐标代入抛物线解析式即可.
(2)如图1中,作PM⊥AB于M,AN⊥CE于N.,先求出PM,再利用$\frac{PM}{BC}$=$\frac{EM}{EB}$,求出EM,PE,由△PME∽△ANE得$\frac{AE}{PE}$=$\frac{EN}{EM}$=$\frac{AN}{PM}$,求出EN、AN即可解决问题.
(3)如图2中,设平移后的抛物线为y=2x2+bx+4,因为△CMQ是等边三角形,所以点Q只能是顶点,顶点Q(-$\frac{b}{4}$,$\frac{32-{b}^{2}}{8}$),根据HQ=$\sqrt{3}$CH,列出方程即可解决问题.
解答 解(1)如图1中,∵四边形ABCD是矩形,
∴BC=AO=5,CO=AB,∠CBA=∠BAO=∠BCO=90°,
∵△CED是由△CEB翻折,
∴CD=AB=5,DE=BE,
在RT△CDO中,∵OD=3,CD=5,
∴CO=$\sqrt{C{D}^{2}-O{D}^{2}}$=4,设BE=ED=x,
在RT△AED中,∵DE2=AE2+AD2,
∴x2=(4-x)2+22,
∵x=$\frac{5}{2}$,
∴点B(5,4),把D(3,0),B(5,4)代入y=2x2+bx+c得$\left\{\begin{array}{l}{18+3b+c=0}\\{50+5b+c=4}\end{array}\right.$解得$\left\{\begin{array}{l}{b=-14}\\{c=24}\end{array}\right.$
∴抛物线解析式为y=2x2-14x+24.
(2)如图1中,作PM⊥AB于M,AN⊥CE于N.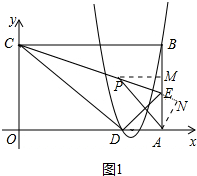
由(1)可知AE=$\frac{3}{2}$,BE=$\frac{5}{2}$
∴$\frac{1}{2}$×AE×PM=$\frac{27}{20}$,
∴PM=$\frac{9}{5}$,
∵PM∥BC,
∴$\frac{PM}{BC}$=$\frac{EM}{EB}$,
∴$\frac{\frac{9}{5}}{5}=\frac{EM}{\frac{5}{2}}$,
∴EM=$\frac{9}{10}$,
∴PE=$\sqrt{P{M}^{2}+M{E}^{2}}$=$\frac{9}{10}\sqrt{5}$,
∵∠PME=∠ANE,∠PEM=∠AEN,
∴△PME∽△ANE,
∴$\frac{AE}{PE}$=$\frac{EN}{EM}$=$\frac{AN}{PM}$,
∴$\frac{\frac{3}{2}}{\frac{9}{10}\sqrt{5}}$=$\frac{EN}{\frac{9}{10}}$=$\frac{AN}{\frac{9}{5}}$,
∴EN=$\frac{3}{10}$$\sqrt{5}$,AN=$\frac{3}{5}\sqrt{5}$,PN=PE+EN=$\frac{6}{5}$$\sqrt{5}$,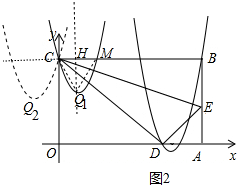
∴tan∠APE=$\frac{AN}{PN}$=$\frac{1}{2}$.
(3)如图2中,设平移后的抛物线为y=2x2+bx+4,
∵△CMQ是等边三角形,
∴点Q只能是顶点,顶点Q(-$\frac{b}{4}$,$\frac{32-{b}^{2}}{8}$),
∴HQ=$\sqrt{3}$CH,
∴$\sqrt{3}$•|(-$\frac{b}{4}$)|=4-$\frac{32-{b}^{2}}{8}$,
∴b=±$\frac{\sqrt{3}}{2}$,
∴满足条件的点Q为:Q1($\frac{\sqrt{3}}{2}$,$\frac{5}{2}$),Q2 (-$\frac{\sqrt{3}}{2}$,$\frac{5}{2}$),
此时抛物线为y=2x2$±\frac{\sqrt{3}}{2}$x+4,
∵点P坐标($\frac{16}{5}$,$\frac{12}{5}$),
显然点P不在其抛物线上.
点评 本题考查二次函数性质、翻折变换、勾股定理、相似三角形的判定和性质、等边三角形的判定和性质,解题的关键是添加辅助线构造直角三角形或相似三角形,第三个问题记住抛物线平移a相同,学会用方程的思想解决问题,属于中考压轴题.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | 8$\sqrt{2}$cm | B. | 4$\sqrt{2}$cm | C. | 8$\sqrt{3}$cm | D. | 4$\sqrt{3}$cm |
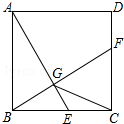 如图,已知正方形ABCD的边长为1,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:
如图,已知正方形ABCD的边长为1,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法: