已知a+b=-8.ab=8.化简$\sqrt{\frac{b}{a}}+\sqrt{\frac{a}{b}}$.并求值．题目和参考答案——青夏教育精英家教网—

题目内容

15．已知a+b=-8，ab=8，化简$\sqrt{\frac{b}{a}}+\sqrt{\frac{a}{b}}$，并求值．

分析首先根据a+b=-8，和ab=8确定a和b的符号，然后对根式进行化简，然后代入求解即可．

解答解：∵a+b=-8＜0，ab=8＞0
∴a＜0，b＜0，
∴原式=$\sqrt{\frac{ab}{{a}^{2}}}$+$\sqrt{\frac{ab}{{b}^{2}}}$
=-$\frac{\sqrt{ab}}{a}$-$\frac{\sqrt{ab}}{b}$
=-$\frac{（a+b）\sqrt{ab}}{ab}$．
则原式=2$\sqrt{2}$．

点评本题考查了根式的化简求值，正确确定a和b的符号是解决本题的关键．

练习册系列答案

假期作业本北京教育出版社系列答案

新课程寒假作业本山西教育出版社系列答案

6．将690 0000用科学记数法表示为6.9×10⁶．

3．

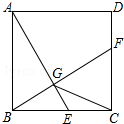如图，已知正方形ABCD的边长为1，E是边BC上的动点，BF⊥AE交CD于点F，垂足为G，连结CG．下列说法：
①AG＞GE；②AE=BF；③点G运动的路径长为$\frac{π}{4}$；④CG的最小值为$\frac{\sqrt{5}}{2}$-1．
其中正确的说法是②③．（把你认为正确的说法的序号都填上）

10．当xx＞-5时，分式$\frac{1}{x+5}$的值是正数．

20．抛物线y=ax²+bx+c（a≠0），对称轴为直线x=2，且经过点P（3，0），则a+b+c的值为（　　）

7．

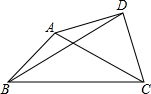如图四边形ABCD中，AB=4$\sqrt{2}$，BC=12，∠ABC=45°，∠ADC=90°，AD=CD，则BD=2$\sqrt{34}$．

4．已知一个多边形的内角和等于它的外角和的2倍，则这个多边形的边数为（　　）

5．如图①，如果四边形ABCD满足AB=AD，CB=CD，∠B=∠D=90°，那么我们把这样的四边形叫做“完美筝形”．
将一张如图①所示的“完美筝形”纸片ABCD先折叠成如图②所示形状，再展开得到图③，其中CE，CF为折痕，∠BCD′=∠ECF=∠FCD，点B′为点B的对应点，点D′为点D的对应点，连接EB′，FD′相交于点O
简单应用：
（1）在平行四边形、矩形、菱形、正方形四种图形中，一定为“完美筝形”的是正方形；
（2）当图③中的∠BCD=120°时，∠AEB′=80°；
（3）当图②中的四边形AECF为菱形时，图③中的四边形OD′CB′是“完美筝形”吗？说明理由．

试题分类