题目内容
1.(1)先化简,再求值:(x+1)2+x(2-x),其中x=$\sqrt{2}$(2)解不等式组$\left\{\begin{array}{l}{2x-4<x}\\{x+9>4x}\end{array}\right.$,并把解集表示在数轴上.
分析 (1)先算乘法,再合并同类项,最后代入求出即可;
(2)先求出每个不等式的解集,再求出不等式组的解集,最后在数轴上表示出来即可.
解答 解:(1)原式=x2+2x+1+2x-x2
=4x+1,
当x=$\sqrt{2}$时,原式=4$\sqrt{2}$+1;
(2)$\left\{\begin{array}{l}{2x-4<x①}\\{x+9>4x②}\end{array}\right.$
∵解不等式①:x<4,
解不等式②:x<3,
∴原不等式组的解集是:x<3,
原不等式组的解集在数轴上表示为: .
.
点评 本题考查了整式的混合运算和求值,也考查了解一元一次不等式组和在数轴上表示不等式组的解集,能正确根据整式的运算法则进行化简是解(1)的关键,能根据不等式的解集求出不等式组的解集是解(2)的关键.

练习册系列答案
相关题目
13.将抛物线y=5x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线的表达式是( )
| A. | y=5(x-2)2+3 | B. | y=5(x+2)2+3 | C. | y=5(x-2)2-3 | D. | y=5(x+2)2-3 |

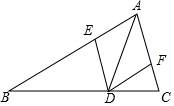 如图,在△ABC中,AD是角平分线,DE∥AC,DF∥AB,求证:四边形AEDF是菱形.
如图,在△ABC中,AD是角平分线,DE∥AC,DF∥AB,求证:四边形AEDF是菱形.