题目内容
10.先化简,再求值:$\frac{1}{x+1}$-$\frac{3-x}{{x}^{2}-6x+9}$$÷\frac{{x}^{2}+x}{x-3}$,其中x=-$\frac{3}{2}$.分析 先算除法,再算减法,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{1}{x+1}$+$\frac{x-3}{(x-3)^{2}}$•$\frac{x-3}{x(x+1)}$
=$\frac{1}{x+1}$+$\frac{1}{x(x+1)}$
=$\frac{x+1}{x(x+1)}$
=$\frac{1}{x}$,
当x=-$\frac{3}{2}$时,原式=-$\frac{2}{3}$.
点评 本题考查的是分式的化简求值及特殊角的三角函数值,在解答此类题目时要把分式化为最简形式,再代入求值.

练习册系列答案
相关题目
11.在△ABC中,已知AB=a2,BC=4a,AC=b2-4,且a,b都是大于3的奇数,则a与b的大小关系是( )
| A. | a>b | B. | a<b | C. | a=b | D. | 不能确定 |
9.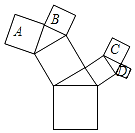 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm、B的边长为5cm、C的边长为5cm,则正方形D的边长为( )| A. | $\sqrt{14}$cm | B. | 4 cm | C. | $\sqrt{15}$cm | D. | 3 cm |
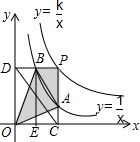 两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$(的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$(的图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形
两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$(的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$(的图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形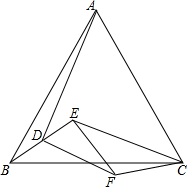 如图,在△ABC中,AB=AC,在△EFC中,EF=FC,且∠BAC+∠EFC=180°,D是BE中点.求证:AD⊥DF.
如图,在△ABC中,AB=AC,在△EFC中,EF=FC,且∠BAC+∠EFC=180°,D是BE中点.求证:AD⊥DF.