Question

19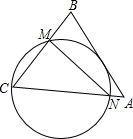．如图，在△ABC中，∠BCA=60°，∠A=45°，AC=2$\sqrt{6}$，经过点C且与边AB相切的动圆与CB，CA分别相交于点M，N，则线段MN长度的最小值是3．

Answer 1

分析 过点C作CF⊥AB于点F，以CF为直径作圆与CB、CA分别相交于点M、N，连接OM、ON，过点O作OE⊥MN于点E，此时线段MN最短，由∠CFA=90°、∠A=45°、AC=2$\sqrt{6}$，即可得出CF的长度，再由∠BCA=60°结合垂径定理即可得出∠MOE=60°，通过解直角三角形即可得出ME的长度，乘2后即可得出结论．

解答 解：过点C作CF⊥AB于点F，以CF为直径作圆与CB、CA分别相交于点M、N，连接OM、ON，过点O作OE⊥MN于点E，如图所示．
∵CF⊥AB，此时圆的直径最小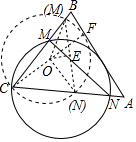，∠MON=2∠MCN为定值，
∴线段MN此时长度最小．
∵∠CFA=90°，∠A=45°，AC=2$\sqrt{6}$，
∴CF=$\frac{\sqrt{2}}{2}$AC=2$\sqrt{3}$．
∵∠BCA=60°，
∴∠MON=120°，
∵OE⊥MN于点E，
∴∠MOE=60°．
∵OM=OC=$\frac{1}{2}$CF=$\sqrt{3}$，∠MOE=60°，
∴ME=$\frac{\sqrt{3}}{2}$OM=$\frac{3}{2}$，
∴MN=2ME=3．
故答案为：3．

点评 本题考查了直线与圆的位置关系、垂径定理以及解直角三角形，找出线段MN取最小值时点M、N的位置是解题的关键．