题目内容
7.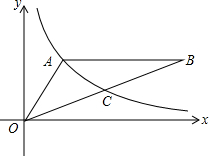 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).(1)确定k的值;
(2)求△OAB的面积.
分析 (1)根据反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A,点A的坐标为(2,3),可以求得k的值;
(2)根据AB∥x轴,可知点A、B的纵坐标相等和OB的中点C,可得点C的纵坐标,由点C在反比例函数的图象上,可得点C的坐标,从而得到点B的坐标,从而可以求得△OAB的面积.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A,点A的坐标为(2,3),
∴$3=\frac{k}{2}$,得k=6,
即k的值是6;
(2)反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),
∴点B的纵坐标是3,
∴点C的纵坐标是$\frac{3}{2}$,
∴$\frac{3}{2}=\frac{6}{x}$,解得x=4,
即点C的坐标是(4,$\frac{3}{2}$),
∴点B的坐标是(8,3),
∴△OAB的面积是$\frac{(8-2)×3}{2}=\frac{6×3}{2}=9$,
即△OAB的面积9.
点评 本题考查反比例函数系数k的几何意义,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
17.若多项式a2+4a+k2是完全平方式,则常数k的值为( )
| A. | 2 | B. | 4 | C. | ±4 | D. | ±2 |
2.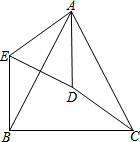 如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.
 如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.
如图,在△ABC中,AB=AC,D是△ABC的外心,连接AD、CD.将△ADC绕点A顺时针旋转到△AEB,连接ED.(1)求证:△AED∽△ABC;
(2)连接BD,判断四边形AEBD的形状并证明.
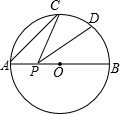 如图,AB是⊙O的直径,AB=2,点C是半圆弧AB上的一点,且∠CAB=40°,点D是BC的中点,点P是直径AB上的动点,则线段PC+PD的最小值是$\sqrt{3}$.
如图,AB是⊙O的直径,AB=2,点C是半圆弧AB上的一点,且∠CAB=40°,点D是BC的中点,点P是直径AB上的动点,则线段PC+PD的最小值是$\sqrt{3}$. 已知反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2).
已知反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2). 如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.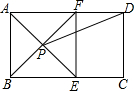 如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.
如图,在矩形ABCD中,AE平分∠BAD,交BC于E,过E做EF⊥AD于F,连接BF交AE于P,连接PD.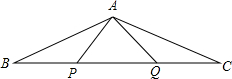 如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.
如图,P,Q是△ABC的边BC上的两点,且BP=QC=AP=AQ.