题目内容
12. 如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
如图,在?ABCD中,已知E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF.(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
分析 (1)利用平行四边形的性质得出∠BAF=∠CFA,进而得出△AEB≌△FEC(AAS),求出答案;
(2)首先得出四边形ABFC是平行四边形,进而得出答案.
解答  (1)证明:∵四边形ABCD是平行四边形,
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DF,
∴∠BAF=∠CFA.
∵E为BC的中点,
∴BE=CE.
在△AEB和△FEC中,
$\left\{\begin{array}{l}{∠BAE=∠CFA}\\{∠AEB=∠FEC}\\{BE=EC}\end{array}\right.$,
∴△AEB≌△FEC(AAS)
∴AB=CF;
(2)解:当BC=AF时,四边形ABFC是矩形,
理由:∵AB=CF,AB‖CF,
∴四边形ABFC是平行四边形,
∵BC=AF,
∴四边形ABFC是矩形.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,正确得出△AEB≌△FEC(AAS)是解题关键.

练习册系列答案
相关题目
3.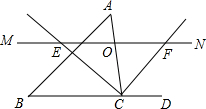 如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
 如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
20.已知菱形的两条对角线长分别为6和8,则该菱形的对称中心到任意一边的距离为( )
| A. | 10 | B. | 5 | C. | 2.5 | D. | 2.4 |
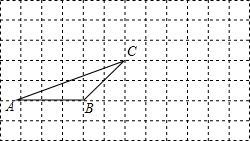 如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).
如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).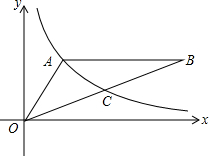 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).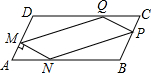 在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.
在一块?ABCD的空地上,划一块?MNPQ进行绿化,如图?MNPQ的顶点在?ABCD的边上,已知∠A=60°,∠AMN=90°,且AM=PC=xm,已知?ABCD的边BC=20m,AB=am,a为大于20m的常数,设四边形MNPQ的面积为Sm2.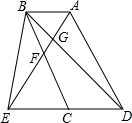 如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE.
如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE.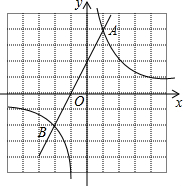 如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).
如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).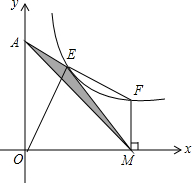 如图,E,F在双曲线y=$\frac{8}{x}$上,FE交y轴于点A,AE=EF,FM⊥x轴于M,求S△AME.
如图,E,F在双曲线y=$\frac{8}{x}$上,FE交y轴于点A,AE=EF,FM⊥x轴于M,求S△AME.