题目内容
15.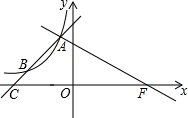 已知反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2).
已知反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2).(1)求a的值;
(2)如图,过点B作直线AB与函数y=$\frac{a+4}{x}$的图象交于点A,与x轴交于点C,且AB=3BC,过点A作直线AF⊥AB,交x轴于点F,求线段AF的长.
分析 (1)由反比例函数y=$\frac{a+4}{x}$(a为常数)的图象经过点B(-4,2),直接利用待定系数法求解即可求得答案;
(2)首先分别过点A、B作x轴的垂线,垂足分别为点D、E,易得△BCD∽△ACE,即可求得A的坐标,由△ACE∽△FAE,即可求得答案.
解答 解:(1)∵图象过点B(-4,2),代入y=$\frac{a+4}{x}$,
∴2=$\frac{a+4}{-4}$,
解得:a=-12;
(2)∵a=-12,
∴反比例函数解析式为$y=-\frac{8}{x}$,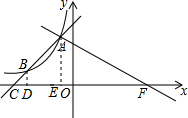 分别过点A、B作x轴的垂线,垂足分别为点D、E,
分别过点A、B作x轴的垂线,垂足分别为点D、E,
∵AB=3BC,
∴$\frac{CB}{CA}=\frac{1}{4}$,BD=2,
∵AD∥BE,
∴△BCD∽△ACE,
∴$\frac{CB}{CA}=\frac{BD}{AE}$,
即$\frac{2}{AE}=\frac{1}{4}$,
∴AE=8.
∴把y=8代入$y=-\frac{8}{x}$,
得x=-1.
∴A(-1,8),
设直线AB解析式为y=kx+b,
把A(-1,8),B(-4,2)代入解析式得,$\left\{\begin{array}{l}-k+b=8\\-4k+b=2\end{array}\right.$,
解得:$\left\{\begin{array}{l}k=2\\ b=10\end{array}\right.$,
∴直线AB解析式为y=2x+10,
当y=0时,2x+10=0,
解得:x=-5,
∴C(-5,0),
∴$AC=\sqrt{A{E^2}+C{E^2}}=\sqrt{{8^2}+{4^2}}=4\sqrt{5}$,
∵AF⊥AB,AE⊥CF,
∴△ACE∽△FAE,
∴$\frac{CE}{AC}=\frac{AE}{AF}$,
∴$\frac{4}{4\sqrt{5}}$=$\frac{8}{AF}$,
解得:AF=8$\sqrt{5}$.
点评 此题属于反比例函数综合题.考查了待定系数求函数解析式以及相似三角形的判定与性质.注意准确作出辅助线是解此题的关键.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案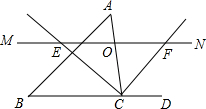 如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )
如图,在锐角△ABC中,点O是AC边上的一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,下列结论中正确的是( )①OE=OF;②CE=CF;③若CE=12,CF=5,则OC的长为6;④当AO=CO时,四边形AECF是矩形.
| A. | ①② | B. | ①④ | C. | ①③④ | D. | ②③④ |
| A. | 10 | B. | 5 | C. | 2.5 | D. | 2.4 |
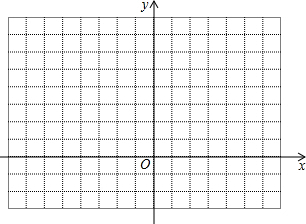 (1)在平面直角坐标系中,描出下列3个点:A (-1,0),B (3,-1),C (4,3);顺次连接A,B,C,组成△ABC.
(1)在平面直角坐标系中,描出下列3个点:A (-1,0),B (3,-1),C (4,3);顺次连接A,B,C,组成△ABC. 如图,已知点A在反比例函数y=$\frac{2}{x}$在第一象限上运动,过点O作OB⊥OA,当tanA=$\sqrt{2}$时,点B恰好落在反比例函数y=$\frac{k}{x}$在第二象限的图象上,则k的值为-4.
如图,已知点A在反比例函数y=$\frac{2}{x}$在第一象限上运动,过点O作OB⊥OA,当tanA=$\sqrt{2}$时,点B恰好落在反比例函数y=$\frac{k}{x}$在第二象限的图象上,则k的值为-4.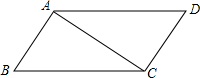 已平行四边形ABCD中∠B=55°,∠2=35°,AD=10,对角线AC=8,求平行四边形ABCD各内角的度数及各边的长.
已平行四边形ABCD中∠B=55°,∠2=35°,AD=10,对角线AC=8,求平行四边形ABCD各内角的度数及各边的长.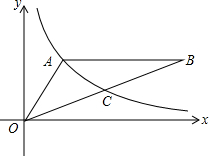 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).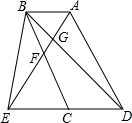 如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE.
如图,已知E为平行四边形ABCD中DC边的延长线上一点,且CE=DC,连接AE分别交BC,BD于点F,G,连接BE.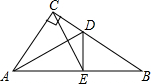 如图,已知在△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB,若∠DCE=∠DEC,已知CD=$\frac{3}{2}$,BC=4
如图,已知在△ABC中,∠ACB=90°,D为BC上一点,DE⊥AB,若∠DCE=∠DEC,已知CD=$\frac{3}{2}$,BC=4