题目内容
20．
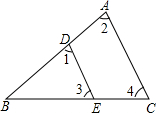
如图，①直线DE，AC被第三条直线BA所截，若DE∥AC，则∠1和∠2是同位角；如果∠1=∠2，则DE∥AC，其理由是同位角相等，两直线平行；
②∠3和∠4是直线DE、AC，被直线BC所截，如果∠3=∠4，则DE∥AC，其理由是内错角相等，两直线平行．
分析 ①根据平行线的性质和判定定理即可得到结论；
②根据平行线的判定定理即可得到结论．
解答 解：①直线DE，AC被第三条直线BA所截，若DE∥AC，则∠1和∠2是同位角；如果∠1=∠2，则DE∥AC，其理由是同位角相等，两直线平行；
②∠3和∠4是直线DE、AC，被直线BC所截，如果∠3=∠4，则DE∥AC，其理由是内错角相等，两直线平行．
故答案为：同位角，DE，AC，同位角相等，两直线平行，DE，AC，BC，DE，AC，内错角相等，两直线平行．
点评 本题考查了平行线的判定和性质，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，
练习册系列答案
相关题目
如图，AB∥CD，AB∥EF，EG平分∠BED，∠B=45°，∠D=30°，求：∠GEF的大小．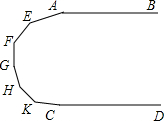
如图，已知AB∥CD，如果在AB和CD间有五个点E、F、G、H、K，说明：∠A+∠C+∠E+∠F+∠G+∠H+∠K=1080°．
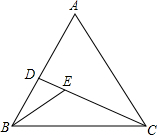如图，在等边△ABC中，D在边AB上，E在CD上，∠BED=60°，DE=2，△ACD的面积6$\sqrt{3}$，则线段CD的长为6．
根据如图，化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{a}^{2}-2ac+{c}^{2}}$+|b+c|．