题目内容
10．已知$\sqrt{15+{x}^{2}}$-$\sqrt{25+{x}^{2}}$=2，求$\sqrt{15+{x}^{2}}$+$\sqrt{25-{x}^{2}}$的值．分析 将$\sqrt{15+{x}^{2}}$-$\sqrt{25+{x}^{2}}$=2，两边平方求得$\sqrt{（15+{x}^{2}）（15-{x}^{2}）}$=18，设y=$\sqrt{15+{x}^{2}}$+$\sqrt{25-{x}^{2}}$，将$\sqrt{15+{x}^{2}}$+$\sqrt{25+{x}^{2}}$平方得到40+2$\sqrt{（15+{x}^{2}）（15-{x}^{2}）}$，将数值代入即可．
解答 解：∵$\sqrt{15+{x}^{2}}$-$\sqrt{25+{x}^{2}}$=2，
∴40-2$\sqrt{（15+{x}^{2}）（15-{x}^{2}）}$=4，
∴$\sqrt{（15+{x}^{2}）（15-{x}^{2}）}$=18，
设y=$\sqrt{15+{x}^{2}}$+$\sqrt{25-{x}^{2}}$，
∴y2=40+2$\sqrt{（15+{x}^{2}）（15-{x}^{2}）}$=40+36=76，
∵y＞0，
∴y=$\sqrt{76}$=2$\sqrt{19}$，
∴$\sqrt{15+{x}^{2}}$+$\sqrt{25-{x}^{2}}$=2$\sqrt{19}$．
点评 本题主要考查了二次根式的意义，算术平方根的意义，由$\sqrt{15+{x}^{2}}$-$\sqrt{25+{x}^{2}}$=2，两边平方求得$\sqrt{（15+{x}^{2}）（15-{x}^{2}）}$=18是解题的关键．
练习册系列答案
相关题目
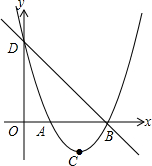如图所示，已知二次函数y=x2-4x+m，它的图象与x轴交于A，B两点（A在B的左侧），与y轴交于点D，且满足OB=OD，顶点为C
已知抛物线y=ax2-2ax-3a（a＜0）．
如图所示，AB∥CD，直线MN分别交AB、CD于E、F，EG平分∠BEF，FG平分∠EFD，EG⊥FG吗？为什么？
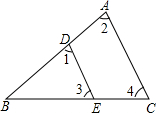如图，