题目内容
5.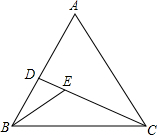 如图,在等边△ABC中,D在边AB上,E在CD上,∠BED=60°,DE=2,△ACD的面积6$\sqrt{3}$,则线段CD的长为6.
如图,在等边△ABC中,D在边AB上,E在CD上,∠BED=60°,DE=2,△ACD的面积6$\sqrt{3}$,则线段CD的长为6.
分析 延长BE交AC边于点F,易证△ACD≌△CBF,得BF=CD,利用三角形的面积求出BF的长度,即为CD的长度.
解答 解:如图,延长BE交AC边于点F,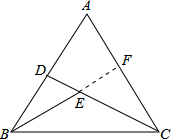
因为∠FCD+∠DCB=60°,∠DEB=∠EBC+∠ECB=60°,
∴∠ACD=∠FBC,
在△ACD和△CBF中,
$\left\{\begin{array}{l}{∠ACB=∠BAC}\\{∠FBC=∠ACD}\\{AC=BD}\end{array}\right.$
∴△ACD≌△CBF(AAS),
∴BF=CD,
∴S△ACD=S△CBF=6$\sqrt{3}$,
∵S△CBF=$\frac{1}{2}$CE•EF•sin60°+$\frac{1}{2}$CE•BE•sin60°=$\frac{1}{2}$CE•BF•sin60°,
∵CE=CD-DE=CD-2,CD=BF,
∴S△CBF=$\frac{1}{2}$(CD-2)•CD•sin60°=6$\sqrt{3}$,
∴CD=6.
故答案为6.
点评 本题考查了等边三角形的性质,三角形全等的判定和性质,以及三角形的面积等,运用三角形全等求得S△ACD=S△CBF是解题的关键.

练习册系列答案
相关题目
17.下列说法错误的是( )
| A. | 两直线平行,内错角相等 | B. | 两直线平行,同旁内角相等 | ||
| C. | 同位角相等,两直线平行 | D. | 平行于同一条直线的两直线平行 |
15.化简$\sqrt{16}$得( )
| A. | ±4 | B. | ±2 | C. | 4 | D. | -4 |
 如图,AB∥CD,∠BAD=70°,∠ADF=20°,∠EFD=130°,探究直线AB与EF有怎样的位置关系?并说明理由.
如图,AB∥CD,∠BAD=70°,∠ADF=20°,∠EFD=130°,探究直线AB与EF有怎样的位置关系?并说明理由.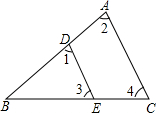 如图,
如图,