题目内容
9. 根据如图,化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{a}^{2}-2ac+{c}^{2}}$+|b+c|.
根据如图,化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{a}^{2}-2ac+{c}^{2}}$+|b+c|.
分析 根据数轴判断出a、b、c的正负情况以及绝对值的大小,再根据二次根式的性质和绝对值的性质化简即可.
解答 解:由图可知,a<0,b<0,c>0且|a|<|c|<|b|,
所以,$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{a}^{2}-2ac+{c}^{2}}$+|b+c|
=-a+(a+b)+(c-a)-(b+c)
=-a+a+b+c-a-b-c
=-a.
点评 本题考查了二次根式的性质与化简,性质:$\sqrt{{a}^{2}}$=|a|=$\left\{\begin{array}{l}{a(a>0)}\\{0(a=0)}\\{-a(a<0)}\end{array}\right.$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列说法错误的是( )
| A. | 两直线平行,内错角相等 | B. | 两直线平行,同旁内角相等 | ||
| C. | 同位角相等,两直线平行 | D. | 平行于同一条直线的两直线平行 |
1.下列四张扑克牌中,属于中心对称的图形是( )


| A. | 红桃7 | B. | 方块4 | C. | 梅花6 | D. | 黑桃5 |
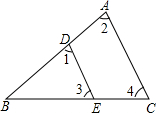 如图,
如图, 如图,在?ABCD中,AE⊥BC,AF⊥CD,E,F为垂足,若∠EAF=59°,则∠B=59度.
如图,在?ABCD中,AE⊥BC,AF⊥CD,E,F为垂足,若∠EAF=59°,则∠B=59度.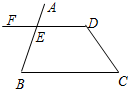 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.