题目内容
 如图:AB⊥BC,CD⊥BC,垂足分别为B,C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为
如图:AB⊥BC,CD⊥BC,垂足分别为B,C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为考点:全等三角形的判定与性质
专题:
分析:如图,证明△ABE≌△BCD,得到BE=CD;结合AB=BC=2BE,即可解决问题.
解答: 解:如图,∵AB⊥BC,AE⊥BD,
解:如图,∵AB⊥BC,AE⊥BD,
∴∠A+∠FEB=∠FBE+∠FEB,
∴∠A=∠FEB;
∵AB⊥BC,CD⊥BC,
∴∠ABE=∠BCD;
在△ABE与△BCD中,
,
∴△ABE≌△BCD(ASA),
∴BE=CD=4;AB=BC;而点E为BC的中点,
∴AB=BC=2BE=8(cm).
故答案为8cm.
 解:如图,∵AB⊥BC,AE⊥BD,
解:如图,∵AB⊥BC,AE⊥BD,∴∠A+∠FEB=∠FBE+∠FEB,
∴∠A=∠FEB;
∵AB⊥BC,CD⊥BC,
∴∠ABE=∠BCD;
在△ABE与△BCD中,
|
∴△ABE≌△BCD(ASA),
∴BE=CD=4;AB=BC;而点E为BC的中点,
∴AB=BC=2BE=8(cm).
故答案为8cm.
点评:该题主要考查了全等三角形的判定及其性质的应用问题;解题的关键是深入观察图形,找出图形中隐含的等量关系或全等关系.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
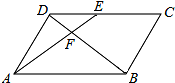 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )| A、2:5 | B、2:3 |
| C、3:5 | D、3:2 |
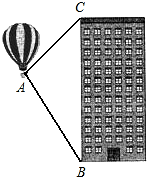 桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据:
桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据: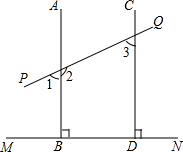 如图,直线AB、CD被直线PQ所截,且都垂直于MN,若∠3=3∠1-∠2,那么∠1=
如图,直线AB、CD被直线PQ所截,且都垂直于MN,若∠3=3∠1-∠2,那么∠1=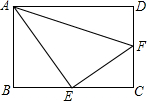 已知:如图,矩形ABCD中,点E是BC的中点,点F在CD上,AE是∠BAF的角平分线.
已知:如图,矩形ABCD中,点E是BC的中点,点F在CD上,AE是∠BAF的角平分线.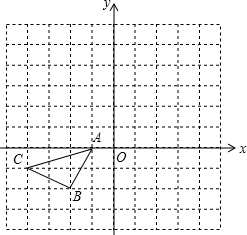 在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: 在△ABC中,AB=9,AC=5,AD是∠BAC的平分线交BC于点D(如图),△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=
在△ABC中,AB=9,AC=5,AD是∠BAC的平分线交BC于点D(如图),△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=