题目内容
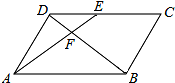 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )| A、2:5 | B、2:3 |
| C、3:5 | D、3:2 |
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:由条件可证明△DEF∽△BAF,结合面积比可求得相似比,可求得答案.
解答:解:∵四边形ABCD为平行四边形,
∴DE∥AB,
∴△DEF∽△BAF,
∴
=(
)2=
,
∴
=
,
故选A.
∴DE∥AB,
∴△DEF∽△BAF,
∴
| S△DEF |
| S△ABF |
| DE |
| AB |
| 4 |
| 25 |
∴
| DE |
| AB |
| 2 |
| 5 |
故选A.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方是解题的关键.

练习册系列答案
相关题目
 如图,直线AB,CD相交于点O,EO⊥CD于点O,FO⊥AB于点O,∠DOF=65°,求∠BOE的度数.
如图,直线AB,CD相交于点O,EO⊥CD于点O,FO⊥AB于点O,∠DOF=65°,求∠BOE的度数.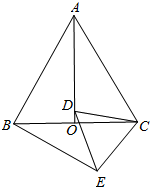 如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
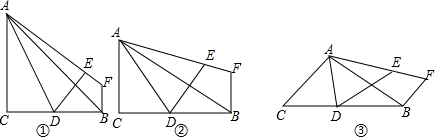
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE. 如图:AB⊥BC,CD⊥BC,垂足分别为B,C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为
如图:AB⊥BC,CD⊥BC,垂足分别为B,C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为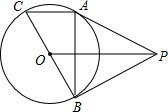 如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.求证:
如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.求证: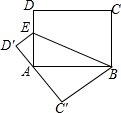 如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为C′,点D的对应点为D′,若点A在C′D′上,且AB=5,BC=4,则AE=
如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为C′,点D的对应点为D′,若点A在C′D′上,且AB=5,BC=4,则AE= 如图所示的电路图中,在开关全部断开的情况下,随机闭合开关S1,S2,S3中的两个,则能让两盏灯泡中至少一盏发光的概率为
如图所示的电路图中,在开关全部断开的情况下,随机闭合开关S1,S2,S3中的两个,则能让两盏灯泡中至少一盏发光的概率为