题目内容
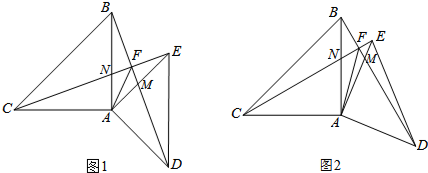
 在△ABC中,AB=9,AC=5,AD是∠BAC的平分线交BC于点D(如图),△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=
在△ABC中,AB=9,AC=5,AD是∠BAC的平分线交BC于点D(如图),△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=| 1 |
| 2 |
考点:翻折变换(折叠问题)
专题:
分析:如图,作辅助线;证明△ADB′∽△DCB′,得到
=
;求出AB′、CB′的长度;进而求出B′D的长度,即可解决问题.
| AB′ |
| B′D |
| B′D |
| CB′ |
解答: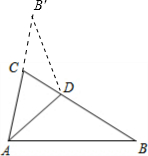 解:如图,由题意得:△ABD≌△AB′D,
解:如图,由题意得:△ABD≌△AB′D,
∴BD=B′D,∠B′AD=∠BAD(设为α);
∵∠B′DC=
∠BAC,
∴∠B′DC=∠B′AD;而∠B′=∠B′,
∴△ADB′∽△DCB′,
∴
=
①;
∵AD平分∠CAB,
∴
=
=
,
设B′D=BD=9λ,则CD=5λ;
∵△ABD≌△AB′D,
∴AB′=AB=9,CB′=9-5=4,代入①并解得:
B′D=6,
∴BD=6.
故答案为6.
 解:如图,由题意得:△ABD≌△AB′D,
解:如图,由题意得:△ABD≌△AB′D,∴BD=B′D,∠B′AD=∠BAD(设为α);
∵∠B′DC=
| 1 |
| 2 |
∴∠B′DC=∠B′AD;而∠B′=∠B′,
∴△ADB′∽△DCB′,
∴
| AB′ |
| B′D |
| B′D |
| CB′ |
∵AD平分∠CAB,
∴
| BD |
| CD |
| AB |
| AC |
| 9 |
| 5 |
设B′D=BD=9λ,则CD=5λ;
∵△ABD≌△AB′D,
∴AB′=AB=9,CB′=9-5=4,代入①并解得:
B′D=6,
∴BD=6.
故答案为6.
点评:该题主要考查了翻折变换的性质、相似三角形的判定及其性质等几何知识点及其应用问题;解题的关键是牢固掌握相似三角形的判定及其性质.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在抛物线y=x2-4x上时,线段BC扫过的面积为
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在抛物线y=x2-4x上时,线段BC扫过的面积为在数0.25,-
,7,0,-3,100中,正数的个数是( )
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠BAD的度数.
如图,在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠BAD的度数. 如图:AB⊥BC,CD⊥BC,垂足分别为B,C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为
如图:AB⊥BC,CD⊥BC,垂足分别为B,C,AB=BC,E为BC的中点,且AE⊥BD于F,若CD=4cm,则AB的长度为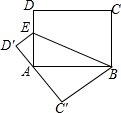 如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为C′,点D的对应点为D′,若点A在C′D′上,且AB=5,BC=4,则AE=
如图,已知点E是长方形ABCD中AD边上一点,将四边形BCDE沿直线BE折叠,折叠后点C的对应点为C′,点D的对应点为D′,若点A在C′D′上,且AB=5,BC=4,则AE=