题目内容
已知，在△ABC中，∠A，∠B，∠C对边分别是a，b，c，a=m-n，b=2
，c=m+n（n＞1），求证：∠C=90°．
| mn |
考点：勾股定理的逆定理
专题：证明题
分析：直接根据勾股定理进行判断即可．
解答：证明：∵（m-n）2+（2
）2=（m+n）2，即a2+b2=c2，
∴△ABC是直角三角形，且∠C=90°．
| mn |
∴△ABC是直角三角形，且∠C=90°．
点评：本题考查的是勾股定理的逆定理，熟知如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形是解答此题的关键．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
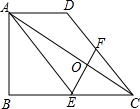已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，BC=2AD，点E是BC的中点、F是CD上的点，联结AE、EF、AC．
某小区现在有一块长方形场地，如图所示，要将这块地划分为四块分别种植兰花、菊花、月季、牵牛花，种植月季的场地长用y表示，宽用x表示．