题目内容

分解因式：（m2+1）2+3（m2+1）-40．
考点：因式分解-十字相乘法等
专题：
分析：直接将m2+1看作整体，进而利用十字相乘法分解因式得出即可．
解答：解：（m2+1）2+3（m2+1）-40
=（m2+1-5）（m2+1+8）
=（m2-4）（m2+9）
=（m+2）（m-2）（m2+9）．
点评：此题主要考查了十字相乘法分解因式，正确应用x2+（p+q）x+pq型的式子的因式分解是解题关键．
练习册系列答案
相关题目
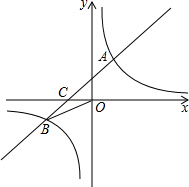已知：如图，在平面直角坐标系中，一次函数y=ax+b （a≠0）的图象与反比例函数y=
k
x
（k≠0）的图象交于一、三象限内的A，B两点，与x轴交于C点，点A的坐标为（2，4），点B的坐标为（n，-2）．
（1）求该反比例函数和一次函数的解析式；
（2）在x轴上有一点E（O点除外），使得△BCE与△BCO的面积相等，求出点E的坐标．
如图，在平面直角坐标系xOy中，点A的坐标为（1，
3
），AB⊥x轴于点B，连结OA，过线段AB上一点F（不与点A重合）的反比例函数y=
k
x
（x＞0）的图象与线段OA交于点E，若直线EF⊥OA，求直线EF的函数解析式．
在平面直角坐标系xOy中，A点坐标为（0，4），C点坐标为（10，0）．若点P在直线y=kx+4上移动时，只存在一个点P使∠OPC=90°，则k的值是
 
．
如图，△ABC的边AB=3，AC=2，Ⅰ、Ⅱ、Ⅲ分别表示以AB、AC、BC为边的正方形，求图中三个阴影部分的面积之和的最大值为
 
．
计算：
（1）492-482
（2）（39
1
2
）2-（10
1
2
）2．
如图，在平面直角坐标系中，点A、B分别在x轴、y轴的正半轴上，点B的坐标是（0，7），且AB=25．△AOB绕某点旋转180°后，点C（36，9）是点B的对应点．
（1）求出△AOB的面积；
（2）写出旋转中心的坐标；
（3）作出△AOB旋转后的三角形．
已知，在△ABC中，∠A，∠B，∠C对边分别是a，b，c，a=m-n，b=2
mn
，c=m+n（n＞1），求证：∠C=90°．
如图，四边形ABCD是平行四边形，M、N是对角线BD上的两点，且BM=DN．求证：四边形AMCN是平行四边形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网