题目内容
12.计算:(1)$\frac{\sqrt{72}}{\sqrt{6}}$;
(2)$\sqrt{6{a}^{2}}$÷$\sqrt{24a}$;
(3)3$\sqrt{20}$÷$\frac{3}{2}$$\sqrt{2\frac{2}{3}}$.
分析 (1)直接利用二次根式除法运算法则化简求出答案;
(2)直接利用二次根式除法运算法则化简求出答案;
(3)直接利用二次根式除法运算法则化简求出答案.
解答 解:(1)原式=$\sqrt{\frac{72}{6}}$=$\sqrt{12}$=2$\sqrt{3}$;
(2)原式=$\sqrt{\frac{6{a}^{2}}{24a}}$=$\sqrt{\frac{a}{4}}$=$\frac{\sqrt{a}}{2}$;
(3)原式=3×$\frac{2}{3}$×$\sqrt{20×\frac{3}{8}}$
=2×$\frac{\sqrt{30}}{2}$
=$\sqrt{30}$.
点评 此题主要考查了二次根式的乘除法,正确化简二次根式是解题关键.

练习册系列答案
相关题目
7.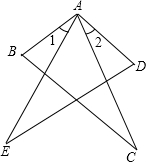 如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
 如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )
如图,要用“SAS”证△ABC≌△ADE,若已知AB=AD,AC=AE,则需要条件是( )| A. | ∠1=∠2 | B. | ∠E=∠C | C. | ∠BAD=∠CAE | D. | ∠B=∠D |
5. 如图,在平面直角坐标系中,点A(2,2),分别以点O,A为圆心,大于$\frac{1}{2}$OA长为半径作弧,两弧交于点P.若点P的坐标为(m,n+1)(m≠1,n≠0),则n关于m的函数表达式为( )
如图,在平面直角坐标系中,点A(2,2),分别以点O,A为圆心,大于$\frac{1}{2}$OA长为半径作弧,两弧交于点P.若点P的坐标为(m,n+1)(m≠1,n≠0),则n关于m的函数表达式为( )
 如图,在平面直角坐标系中,点A(2,2),分别以点O,A为圆心,大于$\frac{1}{2}$OA长为半径作弧,两弧交于点P.若点P的坐标为(m,n+1)(m≠1,n≠0),则n关于m的函数表达式为( )
如图,在平面直角坐标系中,点A(2,2),分别以点O,A为圆心,大于$\frac{1}{2}$OA长为半径作弧,两弧交于点P.若点P的坐标为(m,n+1)(m≠1,n≠0),则n关于m的函数表达式为( )| A. | n=-m+1 | B. | n=-m+2 | C. | n=m+1 | D. | n=m+2 |
 如图,AB⊥BF,CD⊥BF,∠BAF=∠AFE,请说明∠ACD=∠E.
如图,AB⊥BF,CD⊥BF,∠BAF=∠AFE,请说明∠ACD=∠E. 若关于x的二次函数y=ax2+bx+c(a>0,c>1,a、b、c是常数)与x轴交于两个不同的点A(c,0),B(x0,0),与y轴交于点P,其图象顶点为点M,点O为坐标原点,且当0<x<c时,总有y>0.
若关于x的二次函数y=ax2+bx+c(a>0,c>1,a、b、c是常数)与x轴交于两个不同的点A(c,0),B(x0,0),与y轴交于点P,其图象顶点为点M,点O为坐标原点,且当0<x<c时,总有y>0. 如图,在△ABC中,AB=AC,∠ABC=72°,按如下步骤作图:①以点B为圆心,以任意长为半径作弧,分别交AB、BC于点E、F;②分别以点E、F为圆心,以大于$\frac{1}{2}$EF长为半径作弧,两弧相交于点G,连接BG,并延长交AC于点D.则∠ADB的度数为108°.
如图,在△ABC中,AB=AC,∠ABC=72°,按如下步骤作图:①以点B为圆心,以任意长为半径作弧,分别交AB、BC于点E、F;②分别以点E、F为圆心,以大于$\frac{1}{2}$EF长为半径作弧,两弧相交于点G,连接BG,并延长交AC于点D.则∠ADB的度数为108°. 已知,如图,AB和DE是直立在地面上的两根立柱,AB=4m,某一时刻AB在阳光下的投影BC=3m,同一时刻测得DE影长为4.5m,则DE=6m.
已知,如图,AB和DE是直立在地面上的两根立柱,AB=4m,某一时刻AB在阳光下的投影BC=3m,同一时刻测得DE影长为4.5m,则DE=6m.