Question

7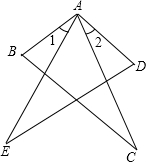．如图，要用“SAS”证△ABC≌△ADE，若已知AB=AD，AC=AE，则需要条件是（　　）

• A． ∠1=∠2
• B． ∠E=∠C
• C． ∠BAD=∠CAE
• D． ∠B=∠D

Answer 1

分析 根据题目中给出的条件AB=AD，AC=AE，要用“SAS”还缺少条件是夹角：∠BAC=∠DAE，筛选答案可选出A．

解答 解：还需条件∠1=∠2，
∵∠1=∠2，
∴∠1+∠EAC=∠2+∠EAC，
即：∠BAC=∠DAE，
在△ABC和△ADE中：
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AE=AC}\end{array}\right.$，
∴△ABC≌△ADE（SAS）．
故选：A．

点评 此题主要考查了全等三角形的判定，关键是要熟记判定定理：SSS，SAS，AAS，ASA．