题目内容
3. 若关于x的二次函数y=ax2+bx+c(a>0,c>1,a、b、c是常数)与x轴交于两个不同的点A(c,0),B(x0,0),与y轴交于点P,其图象顶点为点M,点O为坐标原点,且当0<x<c时,总有y>0.
若关于x的二次函数y=ax2+bx+c(a>0,c>1,a、b、c是常数)与x轴交于两个不同的点A(c,0),B(x0,0),与y轴交于点P,其图象顶点为点M,点O为坐标原点,且当0<x<c时,总有y>0.(1)求常数b的取值范围;
(2)当x1=c时,对于任意给定的常数a、b、c,若点Q($\frac{1}{a}$+c,y0)在对应的二次函数的图象上,过点Q作QK⊥x轴于点K,试问△AQK与△BPO全等吗?证明你的结论;
(3)当x>0时,求证:ax(x+1)+bx(x+2)+c(x+1)(x+2)>0.
分析 (1)根据当0<x<c时,总有y>0,建立不等式求出b的范围;
(2)当x1=c时,对于任意给定的常数a、b、c,若点Q($\frac{1}{a}$+c,y0)在对应的二次函数的图象上,直接确定出AK=BO,QK=PO,即可;
(3)有条件直接得到0<$\frac{x}{x+1}$<1,进而当自变量取时$\frac{x}{x+1}$,必有函数值y>0,化简即可.
解答 解:(1)由题意可得c、x0是方程ax2+bx+c=0的两个根,
所以${x_0}\cdotc=\frac{c}{a}$,所以${x_0}=\frac{1}{a}$.
因为当0<x<c时,总有y>0,所以根据图象必有${x_0}=\frac{1}{a}$>c>0,
所以0<ac<1.
又因为ac2+bc+c=0(a>0,c>0),
所以b=-ac-1.
常数b的取值范围为-2<b<-1.
(2)△AQK与△BPO全等.AK=BO,QK=PO,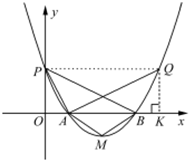
方法一:因为ac2+bc+c=0,b=-ac-1,
所以${y_0}=a{(\frac{1}{a}+c)^2}+b(\frac{1}{a}+c)+c=\frac{1+b}{a}+2c=-c+2c=c$.
从而$\left\{\begin{array}{l}AK=BO\\ QK=PO\\∠POB=∠QAK={90°}\end{array}\right.⇒$△AQK≌△BPO.
方法二:根据对称性可得:点P与点Q关于此抛物线的对称轴对称,所以y0=c.
从而$\left\{\begin{array}{l}AK=BO\\ QK=PO\\∠POB=∠QAK={90°}\end{array}\right.⇒$△AQK≌△BPO.
(3)∵当0<x<1时,总有y>0.显然0<$\frac{x}{x+1}$<1,
∴当自变量取时$\frac{x}{x+1}$,必有函数值y>0. 即有0<$a{(\frac{x}{x+1})^2}+b\frac{x}{x+1}+c$,
所以0<$\frac{ax}{{{{(x+1)}^2}}}+\frac{b}{x+1}+\frac{c}{x}=\frac{a}{{x+\frac{1}{x}+2}}+\frac{b}{x+1}+\frac{c}{x}$<$\frac{a}{x+2}+\frac{b}{x+1}+\frac{c}{x}$.
故当x>0时,ax(x+1)+bx(x+2)+c(x+1)(x+2)>0.
点评 此题是二次函数综合题,主要考查了二次函数的性质,全等三角形的判定,解不等式,解本题的关键是判断出△AQK≌△BPO,和解不等式.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | -$\sqrt{-a}$ | B. | $\sqrt{-a}$ | C. | -$\sqrt{a}$ | D. | -1 |
| A. | y1>y2 | B. | y1≥y2 | C. | y1<y2 | D. | y1≤y2 |
| A. | -3 | B. | 0 | C. | 1 | D. | π |
 如图,已知DE∥BC,AD=15,BD=20,AC=28,则AE=12;S△ADE:S△ABC=9:49.
如图,已知DE∥BC,AD=15,BD=20,AC=28,则AE=12;S△ADE:S△ABC=9:49. 平行四边形ABCD中,BC=4,∠B=60°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AFE,若△AFE与四边形AECD重叠部分的面积是$\frac{17\sqrt{3}}{4}$,则AB=8+3$\sqrt{2}$.
平行四边形ABCD中,BC=4,∠B=60°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AFE,若△AFE与四边形AECD重叠部分的面积是$\frac{17\sqrt{3}}{4}$,则AB=8+3$\sqrt{2}$.