题目内容

7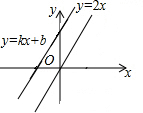．如图，一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点（-1，3），则b的值是5．

分析 根据两条直线相交或平行问题由一次函数y=kx+b的图象与正比例函数y=2x的图象平行得到k=2，然后把点A（-1，3）代入一次函数解析式可求出b的值即可．

解答 解：∵一次函数y=kx+b的图象与正比例函数y=2x的图象平行，
∴k=2，
∴y=2x+b，
把点A（-1，3）代入y=2x+b得-2+b=3，解得b=5，
故答案为5

点评 本题考查了两条直线相交或平行问题：若直线y=k1x+b1与直线y=k2x+b2平行，则k1=k2；若直线y=k1x+b1与直线y=k2x+b2相交，则由两解析式所组成的方程组的解为交点坐标．

练习册系列答案
相关题目
5．已知二元一次方程组$\left\{\begin{array}{l}{ax+by=151}\\{ay+bx=149}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=49}\\{y=51}\end{array}\right.$，则a-b的值是-1．
18．已知M=$\frac{1}{{x}^{2}-9}$，N=$\frac{1}{x+3}$+$\frac{1}{3-x}$，其中x≠±3，则M、N的数量关系为x＞3或x＜-3时，M＞N；当-3＜x＜3时，M＜N．
15．如图①是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图②的形状拼成一个正方形．

（1）请用两种不同的方法求图②中阴影部分的面积．
方法1：（m-n）2方法2：（m+n）2-4mn
（2）观察图②请你写出下列三个代数式：（a+b）2，（a-b）2，ab之间的等量关系．（a-b）2=（a+b）2-4ab
（3）根据（2）题中的等量关系，解决如下问题：
如果a+b=7，ab=-5，求（a-b）2的值．
2．2016年海南马拉松赛于2月28日在三亚市举办，起点为三亚市美丽之冠，赛道为三亚湾路，终点为半山半岛帆船港．在赛道上有A、B两个服务点，现有甲、乙两个服务人员，分别从A，B两个服务点同时出发，沿直线匀速跑向终点C（半山半岛帆船港），如图1所示，设甲、乙两人出发xh后，与B点的距离分别为y甲km、y乙km，y甲、y乙与x的函数关系如图2所示．
（1）从服务点A到终点C的距离为12km，a=0.8h；
（2）求甲乙相遇时x的值；
（3）从甲乙相遇至甲到达终点以前，为更好地一起服务于运动员，两人之间的距离应不超过1km，求此时x的取值范围．
12．如图，直线AB和CD相交于点O，若∠AOD=134°，则∠AOC的度数为（　　）
A．134°B．144°C．46°D．32°
19．如图，平行四边形ABCD中，点E、F在对角线BD上，且BE=DF．求证：
（1）△ABE≌△CDF；
（2）四边形AECF是平行四边形．
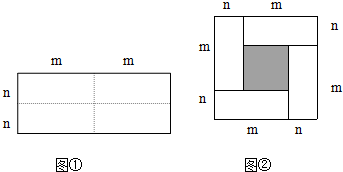
16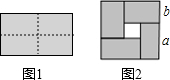．如图1是一个长为2a，宽为2b（a＞b）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图2那样拼成一个正方形，则中间空的部分的面积为（　　）
A．abB．（a+b）2C．（a-b）2D．a2-b2
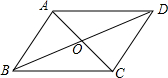17．如图，在?ABCD中，已知AC、BD相交于点O，两条对角线的和为24cm，BC长为8cm，则△AOD的周长=20cm．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网