题目内容
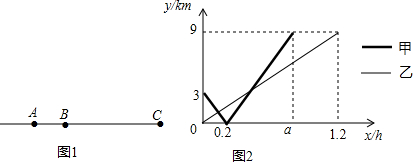
2.2016年海南马拉松赛于2月28日在三亚市举办,起点为三亚市美丽之冠,赛道为三亚湾路,终点为半山半岛帆船港.在赛道上有A、B两个服务点,现有甲、乙两个服务人员,分别从A,B两个服务点同时出发,沿直线匀速跑向终点C(半山半岛帆船港),如图1所示,设甲、乙两人出发xh后,与B点的距离分别为y甲km、y乙km,y甲、y乙与x的函数关系如图2所示.(1)从服务点A到终点C的距离为12km,a=0.8h;
(2)求甲乙相遇时x的值;
(3)从甲乙相遇至甲到达终点以前,为更好地一起服务于运动员,两人之间的距离应不超过1km,求此时x的取值范围.
分析 (1)根据函数图象可以求得从服务点A到终点C的距离和a的值;
(2)根据函数图象可以求得甲乙的函数解析式,由图象和解析式可以求得甲乙相遇时x的值;
(3)由题意和第(2)问中求得的结果可以得到此时x的取值范围.
解答 解:(1)由函数图象可知,
从服务点A到终点C的距离为:3+9=12km,
a=0.2+$\frac{9}{3}$×0.2=0.8h,
故答案为:12,0.8;
(2)设乙的函数解析式为y=kx,
则9=1.2k,得k=$\frac{15}{2}$,
即乙的函数解析式为y=$\frac{15}{2}$x,
设x>0.2时,设y=mx+n,
则$\left\{\begin{array}{l}{0.2m+n=0}\\{0.8m+n=9}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{m=15}\\{n=-3}\end{array}\right.$,
即x>0.2时,甲的函数解析式为:y=15x-3,
由15x-3=$\frac{15}{2}$x,得x=0.4,
即甲乙相遇时x的值是0.4h;
(3)当15x-3-$\frac{15}{2}$x≤1,得x≤$\frac{8}{15}$,
即从甲乙相遇至甲到达终点以前,为更好地一起服务于运动员,两人之间的距离应不超过1km,此时x的取值范围是0.4≤x≤$\frac{8}{15}$.
点评 本题考查一次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.

练习册系列答案
相关题目
13.星星果汁店中的A种果汁比B种果汁每杯贵1元,小彬和同学买了3杯B种果汁,2杯A种果汁,一共花了16元,A种果汁B种果汁每杯分别多少元?设A种果汁的单价为x元,B种果汁的单价为y元,则以下方程组正确的是( )
| A. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y-1}\end{array}\right.$ |
14.下列各组数中,不能构成直角三角形的是( )
| A. | $\sqrt{5}$,$\sqrt{12}$,$\sqrt{13}$ | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 3,4,5 | D. | 6,8,10 |
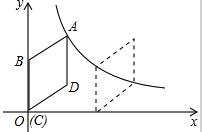 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(x>0)的图象上,菱形ABCD向右平移使点D(4,3)落在反比例函数y=$\frac{k}{x}$(x>0)的图象上,则菱形ABCD平移的距离为$\frac{20}{3}$.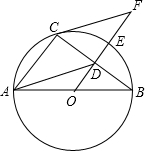 如图,AB为圆O的直径,点C、E在圆上,且点E是弧BC的中点,OE交弦BC于点D,点F在OE的延长线上,且∠BCF=∠BAC,BC=8,DE=2.
如图,AB为圆O的直径,点C、E在圆上,且点E是弧BC的中点,OE交弦BC于点D,点F在OE的延长线上,且∠BCF=∠BAC,BC=8,DE=2.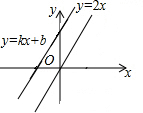 如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点(-1,3),则b的值是5.
如图,一次函数y=kx+b的图象与正比例函数y=2x的图象平行且经过点(-1,3),则b的值是5.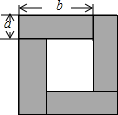 如图是用4个全等的长方形拼成一个“回形”正方形.
如图是用4个全等的长方形拼成一个“回形”正方形.