题目内容
16.先阅读下面的内容,再解决问题,例题:若m2+2mn+2n2-6n+9=0,求m和n的值.
解:∵m2+2mn+2n2-6n+9=0
∴m2+2mn+n2-6n+9=0
∴(m+n)2+(n-3)2=0
∴m+n=0,n-3=0
∴m=-3,n=3
问题:
(1)若△ABC的三边长a,b,c都是正整数,且满足a2+b2-6a-6b+18+|3-c|=0,请问△ABC是什么形状?
(2)已知a,b,c是△ABC的三边长,c是△ABC的最短边且满足a2+b2=12a+8b-52,求c的范围.
分析 (1)先把a2+b2-6a-6b+18+|3-c|=0,配方得到(a-3)2+(b-3)2+|3-c|=0,根据非负数的性质得到a=b=c=3,得出三角形的形状即可;
(2)先根据完全平方公式配方,然后根据非负数的性质列式求出a、b的值,再根据三角形的任意两边之和大于第三边,两边之差小于第三边求出c的取值范围,再根据c是整数求出c的值
解答 解:(1)∵a2+b2-6a-6b+18+|3-c|=0,
∴a2-6a+9+b2-6b+9+|3-c|=0,
∴(a-3)2+(b-3)2+|3-c|=0,
∴a=b=c=3,
∴△ABC是等边三角形.
(2)∵a2+b2=12a+8b-52,
∴a2-12a+36+b2-8b+16=0,
∴(a-6)2+(b-4)2=0,
∴a=6,b=4,
∴2<c<10,
∵c是最短边,
∴2<c≤4.
点评 此题考查了配方法的应用:通过配方,把已知条件变形为几个非负数的和的形式,然后利用非负数的性质得到几个等量关系,建立方程求得数值解决问题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
7. 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | $\sqrt{8}$ | B. | 3 | C. | 4 | D. | $\sqrt{32}$ |
1.下列算式中,正确的有( )
| A. | $\sqrt{3}$+$\sqrt{4}$=$\sqrt{7}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=-$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{1\frac{1}{2}}$÷$\sqrt{\frac{1}{6}}$=3 |
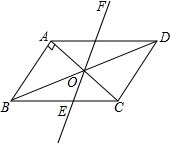 如图,?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
如图,?ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.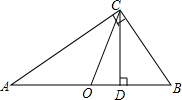 如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.
如图,Rt△ABC中,O为斜边中点,CD为斜边上的高.若OC=$\sqrt{6}$,DC=$\sqrt{5}$,则△ABC的面积是$\sqrt{30}$.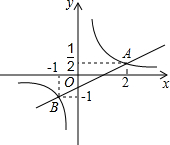 如图,平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)图象相交于A、B两点.
如图,平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)图象相交于A、B两点.