题目内容
5．已知点P（x，y）在第四象限，且到y轴的距离为3，到x轴的距离为5，则点P的坐标是（3，-5）．分析 首先根据点P（x，y）在第四象限，且到y轴的距离为3，可得点P的横坐标是3；然后根据到x轴的距离为5，可得点P的纵坐标是-5，据此求出点P的坐标是多少即可．
解答 解：∵点P（x，y）在第四象限，且到y轴的距离为3，
∴点P的横坐标是3；
∵点P到x轴的距离为5，
∴点P的纵坐标是-5，
∴点P的坐标（3，-5）；
故答案为：（3，-5）．
点评 此题主要考查了点的坐标的确定，要熟练掌握，解答此题的关键是要确定出点P的横坐标和纵坐标各是多少，并要明确：（1）建立了坐标系的平面叫做坐标平面，两轴把此平面分成四部分，分别叫第一象限，第二象限，第三象限，第四象限．坐标轴上的点不属于任何一个象限．（2）坐标平面内的点与有序实数对是一一对应的关系．
练习册系列答案
相关题目
如图，四边形ABCD是平行四边形，E、F是对角线BD上的点，∠1=∠2．求证：AF∥CE且AF=CE．
13．方程3-2（x-5）=9的解是（ ）
| A． | x=-2 | B． | x=2 | C． | x=$\frac{2}{3}$ | D． | x=1 |
20．
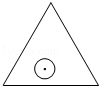如图，一个半径为r的圆形纸片在边长为a$（a≥2\sqrt{3}r）$的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）
如图，一个半径为r的圆形纸片在边长为a$（a≥2\sqrt{3}r）$的等边三角形内任意运动，则在该等边三角形内，这个圆形纸片“不能接触到的部分”的面积是（ ）| A． | $（3\sqrt{3}-π）{r^2}$ | B． | $\frac{{（3\sqrt{3}-π）}}{3}{r^2}$ | C． | $\frac{π}{3}{r^2}$ | D． | πr2 |
如图所示，矩形ABCD沿EF折叠，若∠DEF=72°，则∠AEG的度数为36°．
14．和-2的相反数相等的是（ ）
| A． | -2的平方 | B． | -2的倒数 | C． | -2的绝对值 | D． | 4的平方根 |