题目内容
14.若两个相似三角形的面积之比为1:16,则这两个三角形对应高比为1:4.分析 根据相似三角形的面积的比等于相似比的平方得到两个相似三角形的相似比为1:4,然后根据相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比等于相似比求解.
解答 解:∵两个相似三角形的面积之比为1:16,
∴两个相似三角形的相似比为1:4,
∴这两个三角形对应高比为1:4.
故答案为1:4.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比等于相似比;相似三角形的面积的比等于相似比的平方.

练习册系列答案
相关题目
4.若|x-1|+|y+2|+|z-3|=0,则(x-1)(y+2)(z+3)的值是( )
| A. | 48 | B. | -48 | C. | 0 | D. | 无法计算 |
5.下列说法正确的是( )
| A. | x=2是不等式2x>4的解 | B. | 方程2x=3x没有解 | ||
| C. | 二元一次方程x+y=2有无数组解 | D. | x<0是不等式2x<1的解集 |
9.下列一元二次方程两实数根和为4的是( )
| A. | x2+2x-4=0 | B. | x2+2x+10=0 | C. | x2-4x+4=0 | D. | x2+4x-5=0 |
3.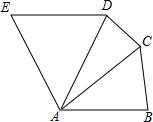 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )| A. | 150° | B. | 160° | C. | 130° | D. | 60° |
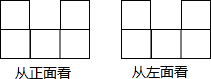 桌上摆着一个由若干个相同正方体组成的几何体,其从正面看和从左面看得到的形状如图所示,那么这个几何体最多可以由13个正方体组成,最少可以由5个正方体组成.
桌上摆着一个由若干个相同正方体组成的几何体,其从正面看和从左面看得到的形状如图所示,那么这个几何体最多可以由13个正方体组成,最少可以由5个正方体组成.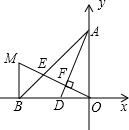 如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.
如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.