��Ŀ����
1���۲��ʽ����$\frac{1}{1��2}$=1-$\frac{1}{2}$����$\frac{1}{2��3}$=$\frac{1}{2}$-$\frac{1}{3}$����$\frac{1}{3��4}$=$\frac{1}{3}$-$\frac{1}{4}$����$\frac{1}{4��5}$=$\frac{1}{4}$-$\frac{1}{5}$������1��������ĸn�ĵ�ʽ��ʾ���㷢�ֵĹ��ɣ���֤���õ�ʽ������
��2��$\frac{1}{1��2}$+$\frac{1}{2��3}$+$\frac{1}{3��4}$+��+$\frac{1}{2016��2017}$=$\frac{2016}{2017}$����ֱ��д�������
���� ��1������������Ȼ�����ĵ������ڸ��Ե����IJ�ó���n����ʽ�����÷�ʽ�����㷨����֤ʽ�ӳ�����
��2����ԭʽ�������Ϲ��ɱ���Ϊ1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+��+$\frac{1}{2016}$-$\frac{1}{2017}$�������������ɵó��𰸣�
��� �⣺��1��������֪����n����ʽΪ$\frac{1}{n��n+1��}$=$\frac{1}{n}$-$\frac{1}{n+1}$��
���ұ�=$\frac{n+1}{n��n+1��}$-$\frac{n}{n��n+1��}$=$\frac{n+1-n}{n��n+1��}$=$\frac{1}{n��n+1��}$=��ߣ�
��$\frac{1}{n��n+1��}$=$\frac{1}{n}$-$\frac{1}{n+1}$��
��2��ԭʽ=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+��+$\frac{1}{2016}$-$\frac{1}{2017}$=1-$\frac{1}{2017}$=$\frac{2016}{2017}$��
�ʴ�Ϊ��$\frac{2016}{2017}$��
���� ������Ҫ�������ֵı仯���ɣ���������ó�������Ȼ�����ĵ������ڸ��Ե����IJ��ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�
�����Ŀ
16�������������y=x2+2������ƽ��1����λ��������ƽ��2����λ����ô�����������ߵı���ʽ�ǣ�������
| A�� | y=��x-1��2 | B�� | y=��x+1��2 | C�� | y=x2+1 | D�� | y=x2+3 |
10��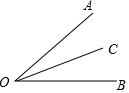 ��ͼ��OCΪ��AOB��һ�����ߣ�������������ȷ��OCƽ�֡�AOB���ǣ�������
��ͼ��OCΪ��AOB��һ�����ߣ�������������ȷ��OCƽ�֡�AOB���ǣ�������
 ��ͼ��OCΪ��AOB��һ�����ߣ�������������ȷ��OCƽ�֡�AOB���ǣ�������
��ͼ��OCΪ��AOB��һ�����ߣ�������������ȷ��OCƽ�֡�AOB���ǣ�������| A�� | ��BOC=$\frac{1}{2}$��AOC | B�� | ��AOC+��COB=��AOB | C�� | ��AOB=2��AOC | D�� | ��COB=��AOB-��AOC |
11���ڳ��ȷֱ�Ϊ4���ס�5���ס�9���ס�12���������߶��У���ѡ�����߶ο�����������εĸ���Ϊ��������
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
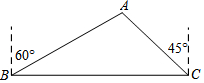 ��ͼ��һ���ִ��������У��ڵ�B����ñ�ƫ��60�㷽����һ����A����������40���ﵽ��C������õ���A�ڵ�C�ı�ƫ��45�㷽���ϣ����ִ�������C��ʱ���ִ������A�ľ���ACΪ���ٺ��
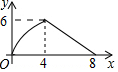
��ͼ��һ���ִ��������У��ڵ�B����ñ�ƫ��60�㷽����һ����A����������40���ﵽ��C������õ���A�ڵ�C�ı�ƫ��45�㷽���ϣ����ִ�������C��ʱ���ִ������A�ľ���ACΪ���ٺ��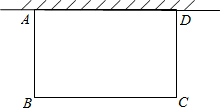 �ڹ�Ԫ�п�չ�ġ�˫������У�ij����С��Ҫ��һ�鿿ǽ��ǽ��15m���Ŀյ�����һ�����λ�ABCD����һ�߿�ǽ���������ܳ�Ϊ40m��դ������ͼ��ʾ������BC�ij�Ϊ������ʱ������ABCD�����Ϊ168m2��
�ڹ�Ԫ�п�չ�ġ�˫������У�ij����С��Ҫ��һ�鿿ǽ��ǽ��15m���Ŀյ�����һ�����λ�ABCD����һ�߿�ǽ���������ܳ�Ϊ40m��դ������ͼ��ʾ������BC�ij�Ϊ������ʱ������ABCD�����Ϊ168m2��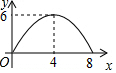
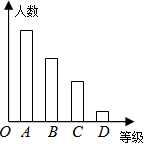 ijУ�Ծ��꼶ѧ�����С��ۺ����ʡ����ۣ����۵Ľ��ΪA���ţ���B�����ã���C���ϸ�D�����ϸ��ĸ��ȼ����ִ��г����������ѧ���ġ��ۺ����ʡ��ȼ���Ϊ�����������ݴ�����������ͼ��ʾ��ͳ��ͼ����֪ͼ�д����ҵ��ĸ������εĸߵı�Ϊ��14��9��6��1�����۽��ΪD�ȼ�����2�ˣ�����ش��������⣺
ijУ�Ծ��꼶ѧ�����С��ۺ����ʡ����ۣ����۵Ľ��ΪA���ţ���B�����ã���C���ϸ�D�����ϸ��ĸ��ȼ����ִ��г����������ѧ���ġ��ۺ����ʡ��ȼ���Ϊ�����������ݴ�����������ͼ��ʾ��ͳ��ͼ����֪ͼ�д����ҵ��ĸ������εĸߵı�Ϊ��14��9��6��1�����۽��ΪD�ȼ�����2�ˣ�����ش��������⣺