Question

9．等腰三角形ABC中，AB=CB=5，AC=8，P为AC边上一动点，PQ⊥AC，PQ与△ABC的腰交于点Q，连结CQ，设AP为x，△CPQ面积为y，则y关于x的函数关系的图象大致是（　　）

• A．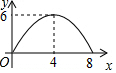
• B．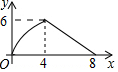
• C．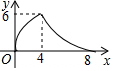
• D．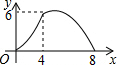

Answer 1

分析 过B作BD⊥AC于D，则AD=CD=4，由勾股定理可得BD=3，再分两种情况进行讨论：当Q在AB上时，求得△CPQ面积y=$\frac{1}{2}$PQ×CP=-$\frac{3}{8}$x²+3x（0≤x＜4）；当Q在BC上时，求得△CPQ面积y=$\frac{1}{2}$PQ×CP=$\frac{3}{8}$x²-6x+24（4≤x≤8），据此判断函数图象即可．

解答 解：过B作BD⊥AC于D，则AD=CD=4，
∴由勾股定理可得，BD=3，
如图所示，当Q在AB上时，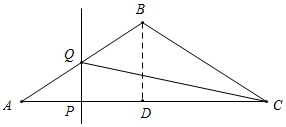

由PQ∥BD，可得$\frac{AP}{AD}$=$\frac{PQ}{DB}$，
∴PQ=$\frac{3}{4}$AP=$\frac{3}{4}$x，
又∵CP=AC-AP=8-x，
∴△CPQ面积y=$\frac{1}{2}$PQ×CP=$\frac{1}{2}$×$\frac{3}{4}$x×（8-x）=-$\frac{3}{8}$x²+3x（0≤x＜4）；
如图所示，当Q在BC上时，CP=8-x，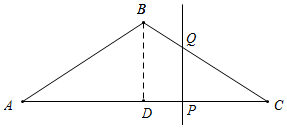

由PQ∥BD，可得PQ=$\frac{3}{4}$CP=$\frac{3}{4}$（8-x），
∴△CPQ面积y=$\frac{1}{2}$PQ×CP=$\frac{1}{2}$×$\frac{3}{4}$（8-x）（8-x）=$\frac{3}{8}$x²-6x+24（4≤x≤8），
∴当0≤x＜4时，函数图象是开口向下的抛物线；当4≤x≤8时，函数图象是开口向上的抛物线．
故选：C．

点评 本题主要考查了动点问题的函数图象，解题时注意：二次函数的图象为抛物线，开口方向由二次项的系数符号决定，用图象解决问题时，要理清图象的含义即会识图．