Question

11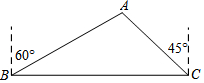．如图，一艘轮船自西向东航行，在点B处测得北偏东60°方向有一灯塔A，继续向东航行40海里到达C处，测得灯塔A在点C的北偏西45°方向上，求轮船行至点C处时，轮船与灯塔A的距离AC为多少海里？

Answer 1

分析 过A作AD⊥BC于D，求出∠ABD=30°，∠ACD=45°=∠DAC，求出AB=2AD，AD=DC，BD=$\sqrt{3}$AD，设AD=DC=x海里，则BD=$\sqrt{3}$x海里，根据BC=40海里得出方程$\sqrt{3}$x+x=40，求出x即可．

解答 解：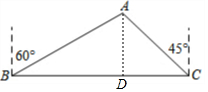
过A作AD⊥BC于D，
则∠ADC=∠ADB=90°，
∵∠ABD=90°-60°=30°，∠ACD=90°-45°=45°=∠DAC，
∴AB=2AD，AD=DC，BD=$\sqrt{3}$AD，
设AD=DC=x海里，则BD=$\sqrt{3}$x海里，
∵BC=40海里，
∴$\sqrt{3}$x+x=40，
解得：x=20$\sqrt{3}$-20，
即AD=DC=（20$\sqrt{3}$-20）海里，
在Rt△ADC中，AC=$\sqrt{2}$AD=$\sqrt{2}$（20$\sqrt{3}$-20）海里=（20$\sqrt{6}$-20$\sqrt{2}$）海里．

点评 本题考查了解直角三角形的应用，能通过解直角三角形求出BD=$\sqrt{3}$AD和AC=$\sqrt{2}$AD是解此题的关键．