题目内容
10.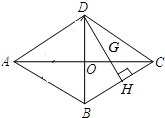 如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥BC于点H,交AC于点G.
如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥BC于点H,交AC于点G.(1)写出两个不全等且与△GHC相似的三角形,并任选其中的一个进行证明;
(2)求GH的长.
分析 (1)根据菱形的性质以及相似三角形的判定方法即可得到和GHC相似的三角形;
(2)根据菱形的对角线互相垂直平分求出OA、OB,再根据勾股定理列式求出AB,然后利用菱形的面积列式计算即可得DH的长,在Rt△DHB中求出BH,然后得出AH,利用tan∠HAG的值,可得出GH的值.
解答 解:(1)△BOC∽△GHC,△GDO∽△GHC,
理由如下:
∵四边形ABCD是菱形,
∴BD⊥CD,
∴∠DOG=90°,
∵DH⊥BC于点H,
∴∠GHC=90°,
∵∠DGO=∠CGH,
∴△GDO∽△GHC;
(2)在菱形ABCD中,AC⊥BD,
∵AC=24cm,BD=18cm,
∴OA=$\frac{1}{2}$AC=$\frac{1}{2}$×16=8,OB=$\frac{1}{2}$BD=$\frac{1}{2}$×12=6cm,
在Rt△AOB中,AB=10cm,
∵DH⊥AB,
∴菱形ABCD的面积=$\frac{1}{2}$AC•BD=AB•DH,
即$\frac{1}{2}$×16×12=10•DH,
解得DH=9.6(cm).
在Rt△DHB中,BH═7.2cm,
则AH=AB-BH=10-7.2=2.8(cm),
∵tan∠HAG=$\frac{GH}{AH}$=$\frac{OB}{OA}$=$\frac{3}{4}$,
∴GH=$\frac{3}{4}$AH=2.1(cm).
点评 本题考查了菱形的性质、解直角三角形及三角函数值的知识,注意菱形的面积等于对角线乘积的一半,也等于底乘高.

练习册系列答案
相关题目
2.二次根式$\sqrt{x-1}$有意义的条件是( )
| A. | x>1 | B. | x≥1 | C. | x<1 | D. | x≤1 |
20.已知a>b,c≠0,下列不等式一定成立的是( )
| A. | ac<bc | B. | c-a<c-b | C. | $\frac{a}{c}$$>\frac{b}{c}$ | D. | a+c<b+c |