题目内容
15.计算题:(1)4$\sqrt{3}-\sqrt{12}$+$\frac{2}{3}\sqrt{27}$-$\frac{1}{2}\sqrt{48}$+$\frac{1}{5}\sqrt{75}$
(2)$\frac{\sqrt{2}}{2}$sin230°+cos260°-2cos245°.
分析 (1)先进行二次根式的化简,然后合并;
(2)分别将特殊角的三角函数值代入,然后化简求解.
解答 解:(1)原式=4$\sqrt{3}$-2$\sqrt{3}$+2$\sqrt{3}$-2$\sqrt{3}$+$\sqrt{3}$
=3$\sqrt{3}$;
(2)原式=$\frac{\sqrt{2}}{2}$×$\frac{1}{4}$+$\frac{1}{4}$-2×$\frac{1}{2}$
=$\frac{\sqrt{2}}{8}$-$\frac{3}{4}$.
点评 本题考查了二次根式的混合运算和特殊角的三角函数值,解答本题的关键是掌握二次根式的化简以及特殊角的三角函数值.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.下列计算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{2}$•$\sqrt{5}$=$\sqrt{10}$ | C. | 2+$\sqrt{2}$=2$\sqrt{2}$ | D. | $\frac{\sqrt{6}}{\sqrt{2}}$=3 |
4.在平面直角坐标系中,点(-4,a2+2)一定在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |


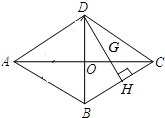 如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥BC于点H,交AC于点G.
如图,四边形ABCD是菱形,对角线AC=16cm,BD=12cm,DH⊥BC于点H,交AC于点G.