题目内容
17.解不等式组:$\left\{\begin{array}{l}{5x-3<4x,①}\\{4(x-1)+3≥2x,②}\end{array}\right.$ 请结合连意填空,完成本题的解答.(1)解不等式①,得x<3;
(2)解不等式②,得x≥$\frac{1}{2}$;
(3)把不等式①和②的解集在数轴上表示出来:

(4)原不等式组的解集为$\frac{1}{2}$≤x<3.
分析 (1)移项、合并同类项即可求解;
(2)去括号、移项、合并同类项、系数化成1即可求解;
(3)把(1)和(2)求得解集在数轴上表示出来即可;
(4)两个解集的公共部分就是不等式组的解集.
解答 解:(1)移项得5x-4x<3,
合并同类项得x<3.
故答案是x<3;
(2)去括号,得4x-4+3≥2x,
移项,得4x-2x≥4-3,
合并同类项得2x≥1,
系数化成1得x≥$\frac{1}{2}$.
故答案是x≥$\frac{1}{2}$;
(3) ;
;
(4)不等式组的解集是:$\frac{1}{2}$≤x<3,
故答案是:$\frac{1}{2}$≤x<3.
点评 本题考查了解一元一次不等式组:求不等式组的解集的过程叫解不等式组.解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
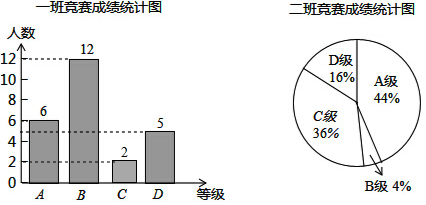
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有21人;
(2)补全下表中空缺的三个统计量:
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有21人;
(2)补全下表中空缺的三个统计量:
| 平均数(分) | 中位数(分) | 众数(分) | |
| 一班 | 77.6 | 80 | 80 |
| 二班 | 77.6 | 70 | 90 |
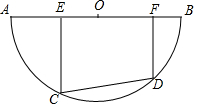 如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.
如图,半圆O的直径AB=10,有一条定长为6的动弦CD在弧AB上滑动(点C、点D分别不与点A、点B重合),点E、F在AB上,EC⊥CD,FD⊥CD.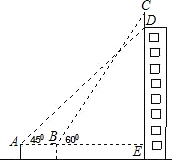 如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)
如图,某幢大楼顶部有一块广告牌CD,在A处测得D点的仰角为45°,在B处测得C点的仰角为60°,A,B,E三点在一条直线上,且与地面平行,若AB=8m,BE=15m,求这块广告牌CD的高度.(取$\sqrt{3}$≈1.73,计算结果保留整数)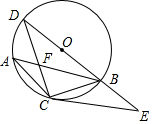 如图,AB是⊙O的弦,C是劣弧$\widehat{AB}$的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
如图,AB是⊙O的弦,C是劣弧$\widehat{AB}$的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.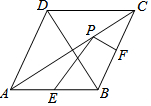 如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )
如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )