Question

7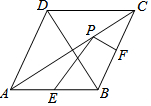．如图，在菱形ABCD中，对角线AC=8，BD=6，点E，F分别是边AB，BC的中点，点P在AC上运动，在运动过程中，存在PE+PF的最小值，则这个最小值是（　　）

• A． 3
• B． 4
• C． 5
• D． 6

Answer 1

分析 设AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，根据菱形的性质推出N是AD中点，P与O重合，推出PE+PF=NF=AB，根据勾股定理求出AB的长即可．

解答 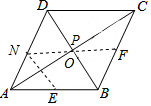解：设AC交BD于O，作E关于AC的对称点N，连接NF，交AC于P，则此时EP+FP的值最小，
∴PN=PE，
∵四边形ABCD是菱形，
∴∠DAB=∠BCD，AD=AB=BC=CD，OA=OC，OB=OD，AD∥BC，
∵E为AB的中点，
∴N在AD上，且N为AD的中点，
∵AD∥CB，
∴∠ANP=∠CFP，∠NAP=∠FCP，
∵AD=BC，N为AD中点，F为BC中点，
∴AN=CF，
在△ANP和△CFP中
∵$\left\{\begin{array}{l}{∠ANP=∠CFP}\\{AN=CF}\\{∠NAP=∠CFP}\end{array}\right.$，
∴△ANP≌△CFP（ASA），
∴AP=CP，
即P为AC中点，
∵O为AC中点，
∴P、O重合，
即NF过O点，
∵AN∥BF，AN=BF，
∴四边形ANFB是平行四边形，
∴NF=AB，
∵菱形ABCD，
∴AC⊥BD，OA=$\frac{1}{2}$AC=4，BO=$\frac{1}{2}$BD=3，
由勾股定理得：AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=5，
故选C．

点评 本题考查了轴对称-最短路线问题，勾股定理，菱形的性质等知识点的应用，关键是理解题意确定出P的位置和求出AB=NF=EP+FP，题目比较典型，综合性比较强，主要培养学生的计算能力．