题目内容
5.等边三角形的边长为1,则它的面积是$\frac{\sqrt{3}}{4}$.分析 利用等边三角形的“三线合一”的性质作辅助线AD⊥BD,然后在Rt△ABD中由勾股定理求得高线AD的长度,最后根据三角形的面积公式求该三角形的面积即可.
解答  解:如图,等边△ABC的边长是1.
解:如图,等边△ABC的边长是1.
过点A作AD⊥BC于点D.则BD=DC=$\frac{1}{2}$BC=$\frac{1}{2}$,
∴在Rt△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\frac{\sqrt{3}}{2}$;
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$.
故答案是:$\frac{\sqrt{3}}{4}$.
点评 本题考查了等边三角形的性质.等边三角形的底边上的高线、中线与顶角的角平分线三线合一.

练习册系列答案
相关题目
13.下列计算正确的是( )
| A. | x2+x2=x4 | B. | $2{x^{-1}}=\frac{1}{2x}$ | C. | (-5x3)2=10x6 | D. | (-x2)3÷(-x)2=-x4 |
20.已知一个阿米巴虫的质量约是0.000005克,下面用科学计数法表示一个阿米巴虫的质量.其中正确的是( )
| A. | 5.0×10-6克 | B. | 5.0×106克 | C. | 5.0×10-5克 | D. | 5.0×105 |
10.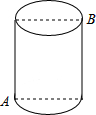 如图,一圆柱高8cm,底面周长为30cm,一只蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高8cm,底面周长为30cm,一只蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
 如图,一圆柱高8cm,底面周长为30cm,一只蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )
如图,一圆柱高8cm,底面周长为30cm,一只蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是( )| A. | 30 cm | B. | 18 cm | C. | 17 cm | D. | 15 cm |
17.瑞安某服装店十月份的营业额为8000元,改进经营措施后营业额稳步上升,十二月份的营业额达到11520元.如果平均每月的增长率为x,则由题意可列出方程为( )
| A. | 8000•2x=11520 | B. | 8000(1+x)=11520 | C. | 8000(1+2x)=11520 | D. | 8000(1+x)2=11520 |
15.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
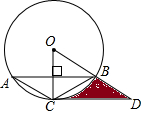 已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由$\widehat{BC}$,线段CD和线段BD所围成图形的阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由$\widehat{BC}$,线段CD和线段BD所围成图形的阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.