题目内容
14.若a2-3a+2=0,则1+6a-2a2=5.分析 先根据a2-3a+2=0得出a2-3a=-2,再代入代数式进行计算即可.
解答 解:∵a2-3a+2=0,
∴a2-3a=-2,
∴原式=-2(a2-3a)+1
=4+1
=5.
故答案为:5.
点评 本题考查的是代数式求值,在解答此类题目时要注意整体代入法的应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
9.(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
| 球的类别 | 无记号 | 有记号 | ||
| 红色 | 黄色 | 红色 | 黄色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
19.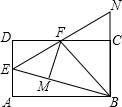 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC,EF交于点N.有下列四个结论:
如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC,EF交于点N.有下列四个结论:
①BF垂直平分EN;
②BF平分∠MFC;
③△DEF∽△FEB;
④tan∠N=$\sqrt{3}$.
其中,将正确结论的序号全部选对的是( )
 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC,EF交于点N.有下列四个结论:
如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC,EF交于点N.有下列四个结论:①BF垂直平分EN;
②BF平分∠MFC;
③△DEF∽△FEB;
④tan∠N=$\sqrt{3}$.
其中,将正确结论的序号全部选对的是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
4.下列各数中,-3的倒数是( )
| A. | 3 | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | -3 |
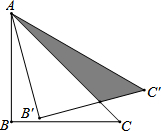 如图,腰长为3的等腰直角三角形ABC绕点A逆时针旋转15°,则图中阴影部分的面积为$\frac{9}{2}$-$\frac{3}{2}$$\sqrt{3}$.
如图,腰长为3的等腰直角三角形ABC绕点A逆时针旋转15°,则图中阴影部分的面积为$\frac{9}{2}$-$\frac{3}{2}$$\sqrt{3}$. 如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)
如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)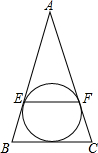 如图,在△ABC中,AB=AC,它的内切圆分别切AB,AC于点E,F,若AB=100,BC=60,求EF的长.
如图,在△ABC中,AB=AC,它的内切圆分别切AB,AC于点E,F,若AB=100,BC=60,求EF的长.