题目内容
9.(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
| 球的类别 | 无记号 | 有记号 | ||
| 红色 | 黄色 | 红色 | 黄色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
分析 (1)根据试验次数和白球的频数可以估算出摸到白球的概率,从而可以得到未放入白球前袋中的小球个数;
(2)①根据表格可以得到袋中红球和黄球的百分比;
②根据表格和题意可以得到袋中的球的数量,然后根据红球所占的百分比可以得到红球的个数.
解答 解:(1)设盒中在未放入白球前共有x个球
$\frac{40}{400}=\frac{2}{2+x}$
解得x=18,
即袋中原来共有18个小球;
(2)由题意可得,
①盒中红球占总球数的百分比是:$\frac{18+2}{18+2+28+2}=\frac{20}{50}=0.4$=40%,
盒中黄球占总球数的百分比是:$\frac{28+2}{28+2+18+2}=\frac{30}{50}=0.6$=60%;
②设盒中有x个球,
$\frac{4}{50}=\frac{8}{x}$,
解得x=100.
100×40%=40个,
即盒中有40个红球.
点评 本题考查模拟实验,解题的关键是明确题意,根据表格中的数据和试验的结果可以计算出相应的概率,找出所求问题需要的条件.

练习册系列答案
相关题目
4.下列算式结果为-2的是( )
| A. | -|-2| | B. | (-2)0 | C. | -(-2) | D. | (-2)-1 |
19.下列运算正确的是( )
| A. | a•a-1=0 | B. | (a2)3=a6 | C. | -2×103=-20000 | D. | a6÷a2=a3 |
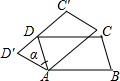 如图,在平行四边形ABCD中,∠BAD=110°,将四边形BCD绕点A逆时针旋转到平行四边形AB′C′D′的位置,旋转角α(0°<α<70°),若C′D′恰好经过点D,则α的度数为40°.
如图,在平行四边形ABCD中,∠BAD=110°,将四边形BCD绕点A逆时针旋转到平行四边形AB′C′D′的位置,旋转角α(0°<α<70°),若C′D′恰好经过点D,则α的度数为40°. 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.