题目内容
19.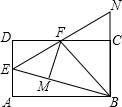 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC,EF交于点N.有下列四个结论:
如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC,EF交于点N.有下列四个结论:①BF垂直平分EN;
②BF平分∠MFC;
③△DEF∽△FEB;
④tan∠N=$\sqrt{3}$.
其中,将正确结论的序号全部选对的是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
分析 由折叠的性质、矩形的性质与角平分线的性质,可证得CF=FM=DF;易求得∠BFE=∠BFN,则可得BF⊥EN;易证得△BEN是等腰三角形,但无法判定是等边三角形;故正确的结论有3个.
解答 解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF,
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF,在△DEF与△CFN中,$\left\{\begin{array}{l}{∠D=∠FCN=90°}\\{DF=CF}\\{∠DFE=∠CFN}\end{array}\right.$,
∴△DFE≌△CFN,
∴EF=FN,
∵∠BFM=90°-∠EBF,∠BFC=90°-∠CBF,
∴∠BFM=∠BFC,
∴BF平分∠MFC;故②正确;
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,
∴BF垂直平分EN,故①正确;
∵∠BFE=∠D=∠FME=90°,
∴∠EFM+∠FEM=∠FEM+∠FBE=90°,
∴∠EFM=∠EBF,
∵∠DFE=∠EFM,
∴∠DFE=∠FBE,
∴△DEF∽△FEB;故③正确;
∵△DFE≌△CFN,∴BE=BN,
∴△EBN是等腰三角形,
∴∠N不一定等于60°,
故④错误.
故选:A.
点评 此题考查了折叠的性质、矩形的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,证得△DFE≌△CFN是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
7.已知x=$\sqrt{3}$+1,y=$\sqrt{3}$-1,则x2+2xy+y2的值为( )
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
4.下面四个数中比-3小的数是( )
| A. | 2 | B. | 0 | C. | -2 | D. | -4 |
11.若a-b=3,则a2-2ab+b2-6的值是( )
| A. | 12 | B. | 6 | C. | 3 | D. | 0 |
 如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为(504,-504).
如图,正方形A1A2A3A4,A5A6A7A8,A9A10A11A12,…,(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)正方形的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…,则顶点A2016的坐标为(504,-504).



