Question

2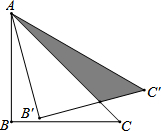．如图，腰长为3的等腰直角三角形ABC绕点A逆时针旋转15°，则图中阴影部分的面积为$\frac{9}{2}$-$\frac{3}{2}$$\sqrt{3}$．

Answer 1

分析 由等腰三角形的性质和已知条件得出∠BAC=45°，∠BAB′=15°，AB′=AB=3，∠B′=∠B=90°，得出∠B′AD=30°，由三角函数求出B′D，求出△AB′D的面积，阴影部分的面积=△AB′C′的面积-△AB′D的面积，即可得出结果．

解答 解：如图所示：
∵将直角边长为3cm的等腰Rt△ABC绕点A逆时针旋转15°得到△AB′C′，
∴∠BAC=45°，∠BAB′=15°，AB′=AB=3，∠B′=∠B=90°，
∴∠B′AD=45°-15°=30°，
∴在Rt△AB′D中，B′D=AB′•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$，
∴S_△AB′D=$\frac{1}{2}$AB′•B′D=$\frac{1}{2}$×3×$\sqrt{3}$=$\frac{3\sqrt{3}}{2}$，
∴阴影部分的面积=$\frac{1}{2}$×3×3-$\frac{3\sqrt{3}}{2}$=$\frac{9}{2}$-$\frac{3\sqrt{3}}{2}$；
故答案为：$\frac{9}{2}$-$\frac{3}{2}$$\sqrt{3}$．

点评 此题考查了旋转的性质以及等腰直角三角形的性质、三角函数．此题难度不大，注意掌握旋转前后图形的对应关系，注意掌握数形结合思想的应用．