题目内容
10．
如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2）、B（1，3）．△AOB绕点O逆时针旋转90°后得到△A1OB1．（1）画出旋转后的图形；
（2）求A1旋转经过的路程．
分析 （1）利用网格特点和旋转的性质画出A、B的对应点A1、B1，从而得到△OA1B1；
（2）由于点A所走过的路线是以点O为圆心，OA为半径，圆心角为90°所对的弧，然后根据弧长公式求解．
解答 解：（1）如图，△A1OB1为所作；
（2）OA=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$，
所以A1旋转经过的路程长=$\frac{90•π•\sqrt{13}}{180}$=$\frac{\sqrt{13}}{2}$π．
点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．
练习册系列答案
阅读快车系列答案
相关题目
18．
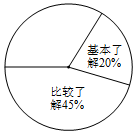为纪念交通大学建校120周年进行宣传，附中中学某年级开展了主题为“交通大学历史知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，整理调查数据制成了如图不完整的表格和扇形统计图．
根据以上提供的信息解答下列问题：
（1）本次问卷调查共抽取的学生数为200人，表中m的值为90．
（2）计算等级为“非常了解”的频数在扇形统计图中对应的圆心角的度数．
（3）若该校有学生1500人，请根据调查结果估计这些学生中“不太了解”交通大学历史的人数约为多少？
为纪念交通大学建校120周年进行宣传，附中中学某年级开展了主题为“交通大学历史知多少”的专题调查活动，采取随机抽样的方式进行问卷调查，问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，整理调查数据制成了如图不完整的表格和扇形统计图．| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 50 | m | 40 | 20 |
（1）本次问卷调查共抽取的学生数为200人，表中m的值为90．
（2）计算等级为“非常了解”的频数在扇形统计图中对应的圆心角的度数．
（3）若该校有学生1500人，请根据调查结果估计这些学生中“不太了解”交通大学历史的人数约为多少？
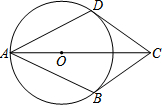如图，已知在四边形ABCD中，AB=AD，BC=CD，点O在对角线AC上，以O为圆心OA为半径的⊙O与CD相切于点D．
如图，∠A=∠D，∠ABC=∠DCB，求证：OA=OD．